Exam 9: Mathematical Modeling Using Differential Equations
Exam 1: Functions and Change204 Questions
Exam 2: Rate of Change: the Derivative132 Questions
Exam 3: Shortcuts to Differentiation178 Questions
Exam 4: Using the Derivative94 Questions
Exam 5: Accumulated Change: the Definite Integral93 Questions
Exam 6: Antiderivatives and Applications122 Questions
Exam 7: Probability68 Questions
Exam 8: Functions of Several Variables134 Questions
Exam 9: Mathematical Modeling Using Differential Equations121 Questions
Exam 10: Geometric Series65 Questions
Select questions type
Look at the slope field labeled I. Consider a solution curve for slope field (I). Which of the answer choices describes the long-run behavior of y at various starting points? 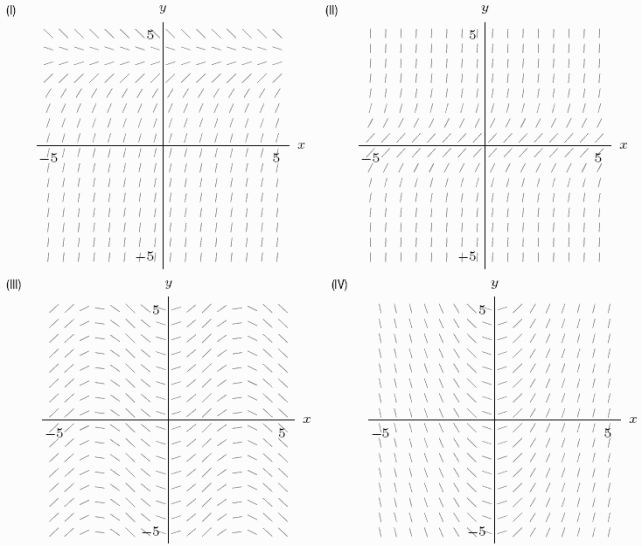
(Multiple Choice)
4.8/5  (33)
(33)
The logistic model for a population's growth is 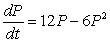 , where P is the size of the population in millions at any time t, measured in years. What is the size of the population when the rate of increase starts to decrease?
, where P is the size of the population in millions at any time t, measured in years. What is the size of the population when the rate of increase starts to decrease?
(Short Answer)
4.7/5  (34)
(34)
Which of the following graphs best describes the temperature in a large North American city over the course of a year? 
(Short Answer)
4.7/5  (33)
(33)
Find the general solution of the separable differential equation: 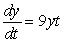
(Short Answer)
4.9/5  (38)
(38)
Water is being pumped into a pool at a rate of 150 gallons per day, and is evaporating at a rate of 0.2% per day. Which is the differential equation for the amount, A, of gallons of water in the pool as a function of time, t, in days?
(Multiple Choice)
4.9/5  (35)
(35)
You invest $2,500 in your nephew's catering business. He guarantees you a minimum return at a continuous interest rate of 4%. Of course, if the business continues to thrive, you will earn at a higher rate.
a) Write a differential equation for the minimum amount, B, of your return on investment at time t.
b) Solve the differential equation.
c) Graph the solution.
(Short Answer)
4.9/5  (34)
(34)
Solve the differential equation using separation of variables. 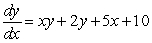
(Multiple Choice)
4.7/5  (38)
(38)
The following figure gives the slope field for 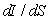 for an SIR epidemic model. Estimate the maximum number of people infected at any one time if the number of susceptibles is initially 400.
for an SIR epidemic model. Estimate the maximum number of people infected at any one time if the number of susceptibles is initially 400. 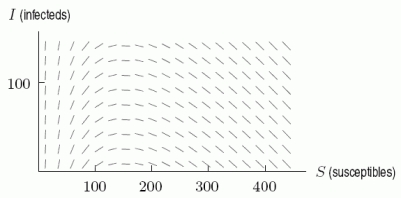
(Multiple Choice)
4.8/5  (26)
(26)
Which of the following slope fields goes with the differential equation 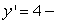 y?
y? 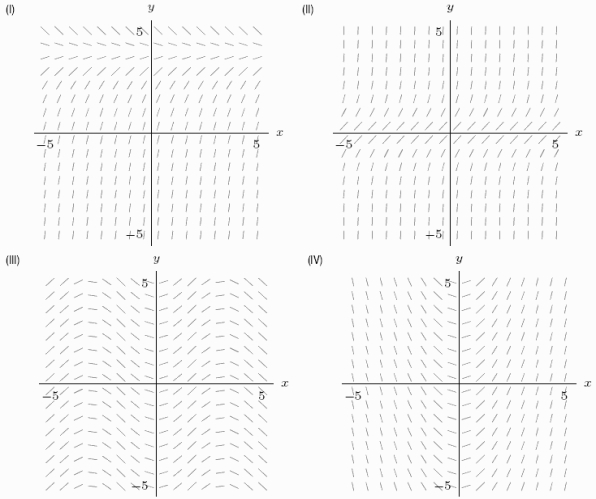
(Short Answer)
4.8/5  (35)
(35)
On January 1, 1879, records show that 500 of a fish called Atlantic striped bass were introduced into the San Francisco Bay. In 1899, the first year fishing for bass was allowed, 100,000 of these bass were caught, representing 10% of the population at the start of 1899. Owing to reproduction, at any moment in time the bass population is growing at a rate proportional to the population at that moment. Assume that when fishing starts in 1899, the rate at which bass are caught is proportional to the square of the population with constant of proportionality 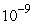 . Write a differential equation satisfied by B(t), for t > 20.
. Write a differential equation satisfied by B(t), for t > 20.
(Multiple Choice)
4.9/5  (44)
(44)
Let f be the number of fruit tree blossoms (in ten thousands) and let b be the number of bees (in hundreds) in an orchard. Suppose f and b satisfy the differential equations 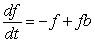 and
and 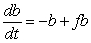 .
Assume f = 3 and b = 1 when t = 0. Use the differential equations to calculate
.
Assume f = 3 and b = 1 when t = 0. Use the differential equations to calculate 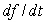 and
and 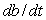 when t = 0, and use these to estimate:
A. the number of fruit tree blossoms when t = 1.
B. the number of bees when t = 1.
when t = 0, and use these to estimate:
A. the number of fruit tree blossoms when t = 1.
B. the number of bees when t = 1.
(Short Answer)
4.9/5  (22)
(22)
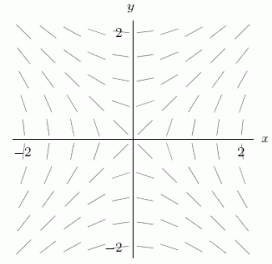
The following figure could be the slope field for the differential equation 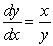 for
for 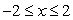 and
and 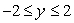 .
. 
(True/False)
4.8/5  (37)
(37)
What is the general solution to the differential equation 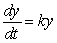 ?
?
(Multiple Choice)
4.9/5  (31)
(31)
In Kenya, the population P for the recent past has obeyed the growth model 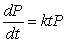 , with t the number of years since 1990. The solution to the differential equation is of the form
, with t the number of years since 1990. The solution to the differential equation is of the form 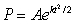 . If the population in 1990 was 24.64 million and in 1992 was 26.16 million, then A = _____ and k = _____. Thus, in the year 1997, the population was approximately _____ million. Round all answers to 2 decimal places.
. If the population in 1990 was 24.64 million and in 1992 was 26.16 million, then A = _____ and k = _____. Thus, in the year 1997, the population was approximately _____ million. Round all answers to 2 decimal places.
(Short Answer)
4.9/5  (29)
(29)
For the first week, the spread of a rumor is proportional to the number of people who have heard the rumor. Find the particular solution to the differential equation for N, the number of people who have heard the rumor as a function of time in days, t, if 15 people have heard it at time t = 0, and 210 people have heard it at time t = 5.
(Multiple Choice)
4.8/5  (27)
(27)
A country experiences a continuous inflation rate of about 5.7% per year. If a t-shirt had a value of $12 in 1995, write a differential equation and use it to find what the t-shirt's value was in 2005. Round to the nearest cent.
(Short Answer)
4.9/5  (28)
(28)
A bank account initially containing $4000 earns interest at a continuous rate of 6% per year. Deposits are made into the account at a constant rate of $500 per year. Which is the differential equation for the balance, B, in the account as a function of time, t, in years?
(Multiple Choice)
4.8/5  (32)
(32)
Showing 101 - 120 of 121
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)