Exam 9: Mathematical Modeling Using Differential Equations
Exam 1: Functions and Change204 Questions
Exam 2: Rate of Change: the Derivative132 Questions
Exam 3: Shortcuts to Differentiation178 Questions
Exam 4: Using the Derivative94 Questions
Exam 5: Accumulated Change: the Definite Integral93 Questions
Exam 6: Antiderivatives and Applications122 Questions
Exam 7: Probability68 Questions
Exam 8: Functions of Several Variables134 Questions
Exam 9: Mathematical Modeling Using Differential Equations121 Questions
Exam 10: Geometric Series65 Questions
Select questions type
The solution to the differential equation 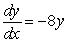 subject to the initial condition that y = 80 when x = 0 is
subject to the initial condition that y = 80 when x = 0 is 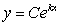 , where k = _____ and C = _____.
, where k = _____ and C = _____.
(Short Answer)
4.9/5  (32)
(32)
Two movie theaters are across the street from each other. Each is doing well, but each would do better if the other were not there. Call the net worth of one theater x and the net worth of the other theater y. Which system of differential equations best models this scenario?
(Multiple Choice)
4.8/5  (32)
(32)
For a new strain of the flu, the differential equations are: 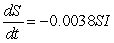 and
and 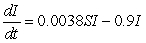 .
What is the threshold value for this strain of the flu? Round down to the nearest whole number.
.
What is the threshold value for this strain of the flu? Round down to the nearest whole number.
(Short Answer)
4.9/5  (40)
(40)
A company earns a continuous annual rate of 11% of its net worth. At the same time, it has expenses of 6.4 million dollars per year. Write a differential equation for the company's worth, W, in millions of dollars as a function of time t, in years. What is the general solution to your differential equation?
(Multiple Choice)
4.8/5  (32)
(32)
Which of the following equations corresponds with the slope field shown below?
I. 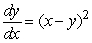 II.
II. 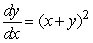 III.
III. 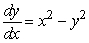 IV. None of them
IV. None of them 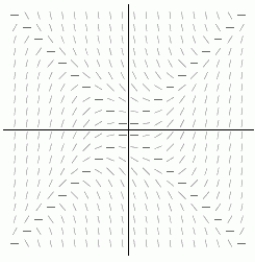
(Short Answer)
4.8/5  (41)
(41)
In a boarding school of 1000 students, at least _____ students should be vaccinated against a flu strain satisfying the differential equations 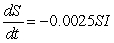
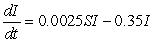 .
.
(Short Answer)
4.7/5  (37)
(37)
Newton's Law of Cooling states that the rate of change of temperature of an object is proportional to the difference between the temperature of the object and the temperature of the surrounding air. A detective discovers a corpse in an abandoned building, and finds its temperature to be 24°C. An hour later its temperature is 16°C. Assume that the air temperature is 8°C, that normal body temperature is 37°C, and that Newton's Law of Cooling applies to the corpse. How many hours has the corpse been dead at the moment it is discovered? Round to 2 decimal places.
(Short Answer)
4.9/5  (37)
(37)
A certain bank account earns interest at the rate of 5% compounded continuously. Money is being withdrawn from the account in a continuous stream at a constant rate of $100,000 per year. Use differential equations to determine what the minimum initial balance should be in order for the account never to be depleted.
(Short Answer)
4.8/5  (40)
(40)
Given that 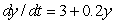 and that
and that 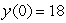 , estimate
, estimate 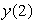 to 1 decimal place by first estimating y(1). Assume that the rate of growth given by
to 1 decimal place by first estimating y(1). Assume that the rate of growth given by 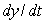 is approximately constant over each unit time interval.
is approximately constant over each unit time interval.
(Short Answer)
4.9/5  (40)
(40)
A fatal infectious disease is introduced into a growing population. Let S denote the number of susceptible people at time t and let I denote the number of infected people at time t. Suppose that, in the absence of the disease, the susceptible population grows at a rate proportional to itself, with constant of proportionality 0.2. People in the infected group die at a rate proportional to the infected population with constant of proportionality 0.05. The rate at which people get infected is proportional to the product of the number of susceptibles and the number of infecteds, with constant of proportionality 0.001. Which of the following systems of differential equations are satisfied by S and I?
(Multiple Choice)
4.9/5  (38)
(38)
On January 1, 1879, records show that 500 of a fish called Atlantic striped bass were introduced into the San Francisco Bay. In 1899, the first year fishing for bass was allowed, 100,000 of these bass were caught, representing 10% of the population at the start of 1899. Owing to reproduction, at any moment in time the bass population is growing at a rate proportional to the population at that moment. Write a differential equation satisfied by B(t), the number of Atlantic striped bass a time t, where t is in years since January 1, 1879 and 0 t < 20 and solve it for B(t).
(Multiple Choice)
4.9/5  (31)
(31)
Solve the initial value problem using separation of variables, and then graph the solution. 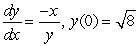
(Short Answer)
4.8/5  (37)
(37)
There is a theory that says the rate at which information spreads by word of mouth is proportional to the product of the number of people who have heard the information and the number who have not. Suppose the total population is N. Which of the following differential equations describe the rate, 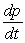 , at which the information spreads by word of mouth?
, at which the information spreads by word of mouth?
(Multiple Choice)
4.7/5  (31)
(31)
The following figure shows the slope field for the differential equation 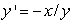 . Guess the equation of the solution curve that goes through the point (0,2).
. Guess the equation of the solution curve that goes through the point (0,2). 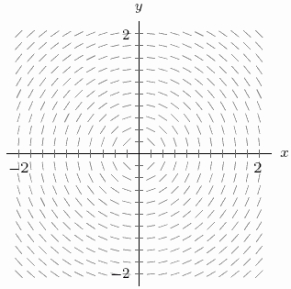
(Short Answer)
4.8/5  (29)
(29)
Find the value of k for which 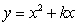 is a solution to the differential equation
is a solution to the differential equation 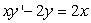 .
.
(Short Answer)
4.8/5  (43)
(43)
A certain bank account earns interest at the rate of 5% compounded continuously. Money is being withdrawn from the account in a continuous stream at a constant rate of $100,000 per year. Write a differential equation modeling how the balance B changes over time. Which of the following is the general solution, given an initial balance of B0?
(Multiple Choice)
4.7/5  (44)
(44)
Two species of insects coexist with each other. Both would do fine on their own. Species x does not do well in the presence of species y. Species y does not do well in the presence of species x. Which of the following systems of equations would best model this scenario?
(Multiple Choice)
4.7/5  (28)
(28)
Showing 41 - 60 of 121
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)