Exam 9: Mathematical Modeling Using Differential Equations
Exam 1: Functions and Change204 Questions
Exam 2: Rate of Change: the Derivative132 Questions
Exam 3: Shortcuts to Differentiation178 Questions
Exam 4: Using the Derivative94 Questions
Exam 5: Accumulated Change: the Definite Integral93 Questions
Exam 6: Antiderivatives and Applications122 Questions
Exam 7: Probability68 Questions
Exam 8: Functions of Several Variables134 Questions
Exam 9: Mathematical Modeling Using Differential Equations121 Questions
Exam 10: Geometric Series65 Questions
Select questions type
Consider the differential equation 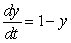 . Is
. Is 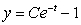 the general solution to the differential equation? If it is not, answer "not the solution". If it is the general solution and if y(3) = 5, what is the constant C?
the general solution to the differential equation? If it is not, answer "not the solution". If it is the general solution and if y(3) = 5, what is the constant C?
(Multiple Choice)
4.8/5  (34)
(34)
A manufacturer of a chocolate beverage mixes liquid chocolate with milk in a large vat containing 450 liters of the mixture that is 20% chocolate initially. The differential equation for A, the amount of chocolate in the vat at time t, follows a "rate in - rate out" model. When chocolate flows in at a rate of 2 liters/min and the mixed beverage flows out at the same rate, you can model the situation with the differential equation 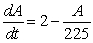 liters/min which can be rewritten as
liters/min which can be rewritten as 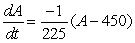 .
a) What is the particular solution to this differential equation?
b) In the long run, how many liters of chocolate will be in the mixture contained in the vat?
.
a) What is the particular solution to this differential equation?
b) In the long run, how many liters of chocolate will be in the mixture contained in the vat?
(Short Answer)
4.7/5  (34)
(34)
A quantity Q satisfies the differential equation 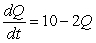 . For what value of Q is the rate of change equal to 0?
. For what value of Q is the rate of change equal to 0?
(Short Answer)
4.9/5  (35)
(35)
Trout are introduced into a stream. Trout is a predator species and therefore has an influence on the population size of other fish. The first figure shows how the trout and other fish populations vary over time. The progress of time is shown by the direction of the arrow. Does the second figure accurately show how the two different populations vary over time? 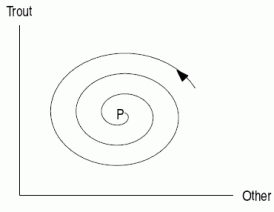
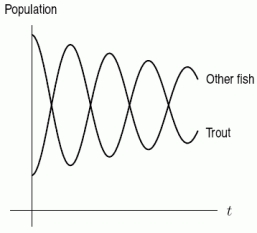
(Short Answer)
4.8/5  (41)
(41)
Suppose 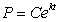 satisfies the differential equation
satisfies the differential equation 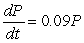 . Then k = _____ and C = _____. If either cannot be determined from the information given, enter "cannot tell".
. Then k = _____ and C = _____. If either cannot be determined from the information given, enter "cannot tell".
(Short Answer)
4.9/5  (26)
(26)
A drug is administered intravenously to a patient at a rate of 12 mg per day. About 40% of the drug in the patient's body is metabolized and leaves the body each day. Which is the differential equation for the amount of the drug, D, in the body as a function of time, t, in days?
(Multiple Choice)
4.8/5  (26)
(26)
Which one(s) of the following are solutions to the differential equation 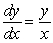 ?
?
(Multiple Choice)
4.9/5  (30)
(30)
Which of the following differential equations goes with the slope field in the figure? 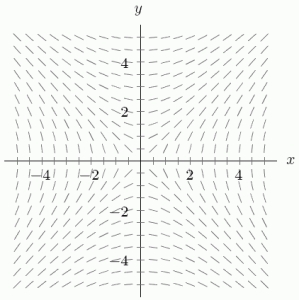
(Multiple Choice)
4.7/5  (47)
(47)
Money in a bank account grows continuously at an annual rate of 4%. Suppose $10,000 is put into an account at time t = 0. If B is the balance in the account after t years, what is the differential equation for B and its solution?
(Multiple Choice)
4.8/5  (37)
(37)
Two minor league baseball teams in the same city compete with each other for fan attendance. Both teams would do well in the absence of the other one, but each team hurts the other team's attendance at games. Create a system of differential equations to model this situation.
(Multiple Choice)
4.8/5  (31)
(31)
Consider three strains of the flu modeled by the following sets of differential equations. Which is the least infectious?
I. 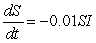
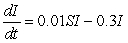 II.
II. 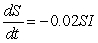
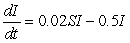 III.
III. 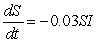
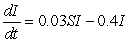
(Short Answer)
4.9/5  (26)
(26)
Which one(s) of the following are solutions to the differential equation 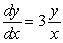 ?
?
(Multiple Choice)
4.8/5  (38)
(38)
Let f be the number of fruit tree blossoms (in ten thousands) and let b be the number of bees (in hundreds) in an orchard. Suppose f and b satisfy the differential equations 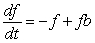 and
and 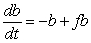 , which correspond to the slope field in the figure. Assume f = 3 and b = 3 when t = 0. What happens to the number of fruit tree blossoms and bees over time?
, which correspond to the slope field in the figure. Assume f = 3 and b = 3 when t = 0. What happens to the number of fruit tree blossoms and bees over time? 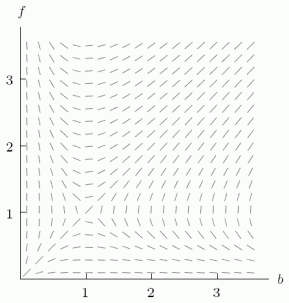
(Multiple Choice)
4.9/5  (36)
(36)
At time t = 0, there are 400 students at a school, 3 of whom have the flu, and 200 of the students have been vaccinated against the flu. Given the differential equation 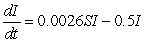 , will the flu spread?
, will the flu spread?
(Short Answer)
4.9/5  (35)
(35)
In a study of the milk drinking habits of a certain population of children, it was found that children drank more and more slowly as they finished a 16 ounce container of milk. Suppose that the rate at which a child drinks is equal to the percentage left to drink, i.e. 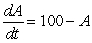 . Find the particular solution given the initial condition A(0) = 0.
. Find the particular solution given the initial condition A(0) = 0.
(Multiple Choice)
4.8/5  (32)
(32)
Bees and flowers help each other, and each needs the other in order to survive. Which (if any) of the following systems of differential equations could model the interaction between bees and flowers, with either species being x or y? Select all that apply.
(Multiple Choice)
4.7/5  (30)
(30)
For a new strain of the flu, the differential equations are: 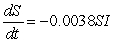 and
and 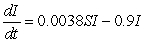 . What is
. What is 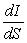 ?
?
(Multiple Choice)
4.9/5  (26)
(26)
Find the solution to the differential equation 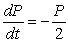 , subject to the initial condition
, subject to the initial condition 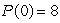 .
.
(Multiple Choice)
4.8/5  (27)
(27)
Showing 81 - 100 of 121
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)