Exam 14: Multiple Integration
Exam 1: Preparation for Calculus125 Questions
Exam 2: Limits and Their Properties85 Questions
Exam 3: Differentiation193 Questions
Exam 4: Applications of Differentiation154 Questions
Exam 5: Integration184 Questions
Exam 6: Differential Equations93 Questions
Exam 7: Applications of Integration119 Questions
Exam 8: Integration Techniques and Improper Integrals130 Questions
Exam 9: Infinite Series181 Questions
Exam 10: Conics, Parametric Equations, and Polar Coordinates114 Questions
Exam 11: Vectors and the Geometry of Space130 Questions
Exam 12: Vector-Valued Functions85 Questions
Exam 13: Functions of Several Variables173 Questions
Exam 14: Multiple Integration143 Questions
Exam 15: Vector Anal142 Questions
Select questions type
Find the Jacobian for the change of variables given below. 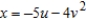 ,
, 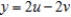
(Multiple Choice)
4.9/5  (33)
(33)
Sketch the region R of integration and then switch the order of integration for the following integral. 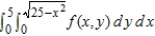
(Multiple Choice)
4.9/5  (40)
(40)
The area of a region R is given by the iterated integrals 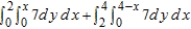 . Switch the order of integration and show that both orders yield the same area. What is this area?
. Switch the order of integration and show that both orders yield the same area. What is this area?
(Multiple Choice)
4.9/5  (47)
(47)
Use a change of variables to find the volume of the solid region lying below the surface 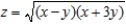 and above the plane region R: region bounded by the parallelogram with vertices
and above the plane region R: region bounded by the parallelogram with vertices 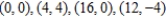 . Round your answer to two decimal places.
. Round your answer to two decimal places.
(Multiple Choice)
4.8/5  (34)
(34)
Find the area of the surface for the portion of the paraboloid 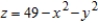 in the first octant.
in the first octant.
(Multiple Choice)
4.7/5  (28)
(28)
Set up and evaluate a double integral to find the volume of the solid bounded by the graphs of the equations 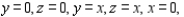 and
and 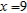 .
.
(Multiple Choice)
4.7/5  (33)
(33)
Use spherical coordinates to find the volume of the solid inside the torus given by 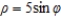 .
.
(Multiple Choice)
5.0/5  (29)
(29)
Use a double integral to find the volume of the indicated solid. 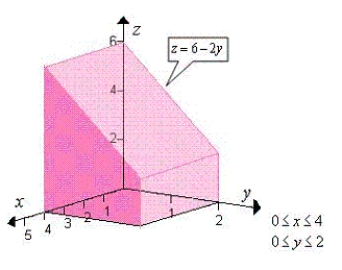
(Multiple Choice)
4.9/5  (40)
(40)
Find the centroid of the solid region bounded by the graphs of the equations. Use a computer algebra system to evaluate the triple integral. (Assume uniform density and find the center of mass.) 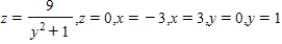
(Multiple Choice)
4.9/5  (37)
(37)
Convert the integral below from rectangular coordinates to both cylindrical and spherical coordinates, and evaluate the simpler iterated integral. 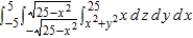
(Multiple Choice)
4.8/5  (44)
(44)
Evaluate the following iterated integral by converting to polar coordinates. 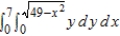
(Multiple Choice)
4.8/5  (30)
(30)
Use a triple integral to find the volume of the solid shown below. 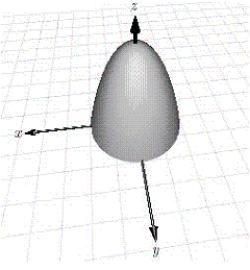
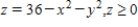
(Multiple Choice)
4.8/5  (38)
(38)
Evaluate the following iterated integral by converting to polar coordinates. 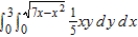
(Multiple Choice)
4.7/5  (29)
(29)
Use cylindrical coordinates to find the volume of the solid inside the sphere 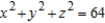 and above the upper nappe of the cone
and above the upper nappe of the cone 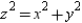 .
.
(Multiple Choice)
4.8/5  (27)
(27)
Find the average value of 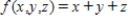 over the region Q, where Q is a tetrahedron in the first octant with vertices
over the region Q, where Q is a tetrahedron in the first octant with vertices 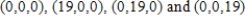 . The average value of a continuous function
. The average value of a continuous function 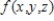 over a solid region Q is
over a solid region Q is 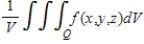 , where V is the volume of the solid region Q.
, where V is the volume of the solid region Q.
(Multiple Choice)
4.8/5  (40)
(40)
Set up a double integral that gives the area of the surface of the graph of f over the region R. 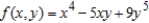
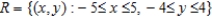
(Multiple Choice)
4.9/5  (32)
(32)
Find the mass of the lamina described by the inequalities 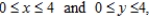 given that its density is
given that its density is 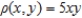 (Hint: Some of the integrals are simpler in polar coordinates.)
(Hint: Some of the integrals are simpler in polar coordinates.)
(Multiple Choice)
4.8/5  (25)
(25)
Showing 101 - 120 of 143
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)