Exam 14: Multiple Integration
Exam 1: Preparation for Calculus125 Questions
Exam 2: Limits and Their Properties85 Questions
Exam 3: Differentiation193 Questions
Exam 4: Applications of Differentiation154 Questions
Exam 5: Integration184 Questions
Exam 6: Differential Equations93 Questions
Exam 7: Applications of Integration119 Questions
Exam 8: Integration Techniques and Improper Integrals130 Questions
Exam 9: Infinite Series181 Questions
Exam 10: Conics, Parametric Equations, and Polar Coordinates114 Questions
Exam 11: Vectors and the Geometry of Space130 Questions
Exam 12: Vector-Valued Functions85 Questions
Exam 13: Functions of Several Variables173 Questions
Exam 14: Multiple Integration143 Questions
Exam 15: Vector Anal142 Questions
Select questions type
Suppose the Cobb-Douglas production function for an automobile manufacturer is 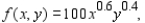 where x is the number of units of labor and y is the number of units of capital. Estimate the average production level if the number of units of labor x varies between 200 and 275 and the number of units of capital y varies between 300 and 375. Round your answer to two decimal places.
where x is the number of units of labor and y is the number of units of capital. Estimate the average production level if the number of units of labor x varies between 200 and 275 and the number of units of capital y varies between 300 and 375. Round your answer to two decimal places.
(Multiple Choice)
4.9/5  (34)
(34)
Find the mass of the lamina bounded by the graphs of the equations 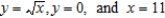 for the density
for the density 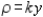 .
.
(Multiple Choice)
4.8/5  (40)
(40)
Consider the region R in the xy-plane bounded by the ellipse 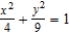 and the transformation
and the transformation 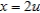 and
and 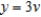 . Find the area of the ellipse. Round your answer to two decimal places.
. Find the area of the ellipse. Round your answer to two decimal places.
(Multiple Choice)
4.8/5  (40)
(40)
Use an iterated integral to find the area of the region bounded by 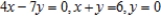 .
.
(Multiple Choice)
4.8/5  (41)
(41)
Set up a double integral that gives the area of the surface on the graph of  over the region
over the region 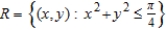 .
.
(Multiple Choice)
4.8/5  (30)
(30)
Use a double integral to find the volume of the indicated solid. 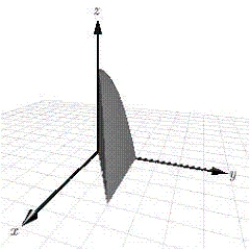
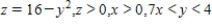
(Multiple Choice)
4.8/5  (37)
(37)
Find the area of the portion of the surface 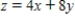 that lies above the region
that lies above the region 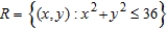 .
.
(Multiple Choice)
4.9/5  (38)
(38)
Use a double integral to find the area of the shaded region as shown in the figure below. 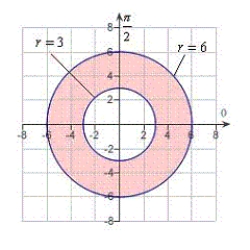
(Multiple Choice)
4.8/5  (39)
(39)
Set up a triple integral for the volume of the solid bounded by 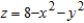 and
and 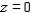 .
.
(Multiple Choice)
4.8/5  (27)
(27)
Use polar coordinates to describe the region as shown in the figure below: 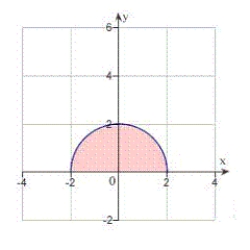
(Multiple Choice)
4.9/5  (26)
(26)
Use a double integral to find the volume of the indicated solid. 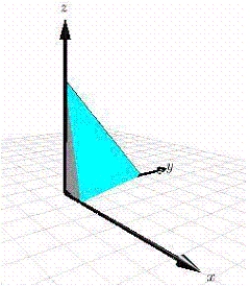
(Multiple Choice)
4.9/5  (39)
(39)
Find the Jacobian 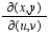 for the following change of variables:
for the following change of variables: 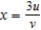 ,
, 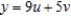
(Multiple Choice)
4.9/5  (28)
(28)
Sketch the solid whose volume is given by the iterated integral given below and use the sketch to rewrite the integral using the indicated order of integration. 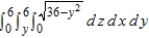 Rewrite the integral using the order
Rewrite the integral using the order 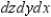 .
.
(Multiple Choice)
4.7/5  (34)
(34)
Find the area of the surface given by 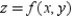 over the region R.
over the region R. 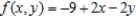
R: square with vertices
R: square with vertices 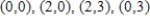
(Multiple Choice)
4.9/5  (28)
(28)
Use cylindrical coordinates to find the volume of the solid bounded above by 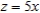 and below by
and below by 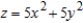 .
.
(Multiple Choice)
4.8/5  (41)
(41)
Set up a double integral that gives the area of the surface of the graph of f over the region R. 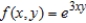
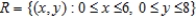
(Multiple Choice)
4.8/5  (40)
(40)
Showing 41 - 60 of 143
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)