Exam 6: Applications of Trigonometry
Exam 1: Functions and Graphs362 Questions
Exam 2: Polynomial, Power, and Rational Functions494 Questions
Exam 3: Exponential, Logistic, and Logarithmic Functions350 Questions
Exam 4: Trigonometric Functions522 Questions
Exam 5: Analytic Trigonometry313 Questions
Exam 6: Applications of Trigonometry333 Questions
Exam 7: Systems and Matrices354 Questions
Exam 8: Analytic Geometry in Two and Three Dimensions167 Questions
Exam 9: Discrete Mathematics154 Questions
Exam 10: Statistics and Probability147 Questions
Exam 11: An Introduction to Calculus: Limits, Derivatives, and Integrals167 Questions
Exam 12: Prerequisites382 Questions
Select questions type
Find the rectangular coordinates of the point with the given polar coordinates.
-
(Multiple Choice)
4.8/5  (33)
(33)
Find the product or quotient. Write the answer in standard form.
-
(Multiple Choice)
4.9/5  (43)
(43)
Solve the problem.
-The locations, given in polar coordinates, of two ships are and . Find the distance between the two ships.
(Multiple Choice)
4.8/5  (39)
(39)
The polar coordinates of point P are given. Find all of its polar coordinates.
-
(Multiple Choice)
4.9/5  (40)
(40)
Find the indicated roots. Write the answer in polar form.
-Fifth roots of
(Multiple Choice)
4.9/5  (38)
(38)
Give a geometric interpretation of what happens to a complex number when it is squared. Describe what
happens to the argument and to the distance from the origin. Will the distance from the origin increase,
decrease, or remain the same?
(Essay)
5.0/5  (36)
(36)
Find the component form and magnitude of the indicated vector.
-Given that and , find the component form and magnitude of the vector .
(Multiple Choice)
4.8/5  (44)
(44)
A directed line segment from to is equivalent to a directed line segment from to the point . Write an expression for the coordinates of the point .
(Multiple Choice)
4.9/5  (36)
(36)
Solve the problem.
-A rectangle has its center at the origin. It has two sides of length 4 a which are parallel to the horizontal axis and two sides of length 2 a parallel to the vertical axis. Find polar coordinates of the vertices.
(Multiple Choice)
4.9/5  (42)
(42)
Determine if the graph is symmetric about the x-axis, the y-axis, or the origin.
-
(Multiple Choice)
4.8/5  (40)
(40)
Determine two pairs of polar coordinates for the point with 0° ≤θ < 360°.
-
(Multiple Choice)
4.7/5  (36)
(36)
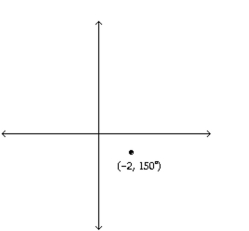
Find the rectangular coordinates of the point with the given polar coordinates.
-
(Multiple Choice)
4.7/5  (35)
(35)
Express the indicated roots of unity in standard form a + bi.
-Fourth roots of unity
(Multiple Choice)
4.9/5  (40)
(40)
Determine whether the vectors u and v are parallel, orthogonal, or neither.
-
(Multiple Choice)
4.8/5  (38)
(38)
Determine two pairs of polar coordinates for the point with 0° ≤θ < 360°.
-
(Multiple Choice)
4.9/5  (32)
(32)
Analyze the graph of the given polar curve. Include the following information: If possible, describe the shape of the
graph (circle, rose curve, limacon, etc.), and state the domain, range, and maximum r-value of the graph. State whether the
graph is continuous and whether it is bounded. Describe any symmetry that the graph has. Give the equations of any
asymptotes or state that the graph has no asymptotes.
-
(Essay)
4.7/5  (41)
(41)
Showing 281 - 300 of 333
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)