Exam 2: Polynomial, Power, and Rational Functions
Exam 1: Functions and Graphs362 Questions
Exam 2: Polynomial, Power, and Rational Functions494 Questions
Exam 3: Exponential, Logistic, and Logarithmic Functions350 Questions
Exam 4: Trigonometric Functions522 Questions
Exam 5: Analytic Trigonometry313 Questions
Exam 6: Applications of Trigonometry333 Questions
Exam 7: Systems and Matrices354 Questions
Exam 8: Analytic Geometry in Two and Three Dimensions167 Questions
Exam 9: Discrete Mathematics154 Questions
Exam 10: Statistics and Probability147 Questions
Exam 11: An Introduction to Calculus: Limits, Derivatives, and Integrals167 Questions
Exam 12: Prerequisites382 Questions
Select questions type
Write the word or phrase that best completes each statement or answers the question.
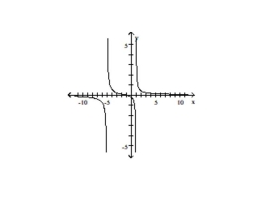
Graph the rational function and analyze it in the following way: find the intercepts, asymptotes, use limits to describe the
behavior at the vertical asymptotes and the end behavior. Find the domain and range. Determine where the function is
continuous and where it is increasing and decreasing. Find any local extrema.
-
Free
(Essay)
4.7/5  (34)
(34)
Correct Answer:
-intercept: -intercept:
Vertical asymptotes:
Horizontal asymptote: 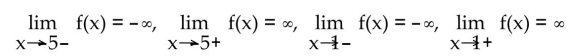
Domain:
Range:
Continuity: all
No local extrema
Decreasing on:
Find the axis of the graph of the function.
-
Free
(Multiple Choice)
4.9/5  (38)
(38)
Correct Answer:
B
Solve the problem.
-An open-top rectangular box has a square base and it will hold 106 cubic centimeters (cc). Each side has length , and it has a height of . Its surface area is given by
Graph the function on the interval .
Free
(Multiple Choice)
4.9/5  (33)
(33)
Correct Answer:
D
Use limits to describe the behavior of the rational function near the indicated asymptote.
-
Describe the behavior of the function near its vertical asymptote.
(Multiple Choice)
4.8/5  (42)
(42)
Solve the problem.
-A rectangular piece of cardboard measuring 17 inches by 45 inches is to be made into a box with an open top by cutting equal size squares from each corner and folding up the sides. Let represent the length of a side of each such square. For what value of will the volume be a maximum? If necessary, round to 2 decimal places.
(Multiple Choice)
4.8/5  (38)
(38)
Choose the one alternative that best completes the statement or answers the question.
Describe how to obtain the graph of the given monomial function from the graph of g(x) = xn with the same power n.
-
(Multiple Choice)
4.9/5  (44)
(44)
Graph the function in a viewing window that shows all of its extrema and x-intercepts.
-
(Multiple Choice)
4.9/5  (33)
(33)
Find a polynomial of degree 3 with real coefficients that satisfies the given conditions.
-Zeros:
(Multiple Choice)
4.9/5  (37)
(37)
Describe how the graph of the given function can be obtained by transforming the graph of the reciprocal function f(x) =
1/x.
-
(Multiple Choice)
4.9/5  (37)
(37)
Describe how the graph of the given function can be obtained by transforming the graph of the reciprocal function f(x) =
1/x.
-
(Multiple Choice)
4.9/5  (42)
(42)
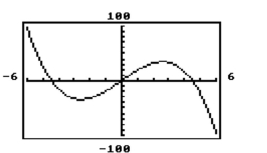
Match the given graph with its polynomial function.Choose the one alternative that best completes the statement or answers the question.
-
(Multiple Choice)
4.8/5  (35)
(35)
Find the requested function.
-Find the cubic function with the given table of values.
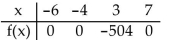
(Multiple Choice)
4.8/5  (27)
(27)
Determine if the function is a power function. If it is, then state the power and constant of variation.
-
(Multiple Choice)
4.8/5  (35)
(35)
Divide using synthetic division, and write a summary statement in fraction form.
-
(Multiple Choice)
4.8/5  (31)
(31)
Showing 1 - 20 of 494
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)