Exam 11: An Introduction to Calculus: Limits, Derivatives, and Integrals
Exam 1: Functions and Graphs362 Questions
Exam 2: Polynomial, Power, and Rational Functions494 Questions
Exam 3: Exponential, Logistic, and Logarithmic Functions350 Questions
Exam 4: Trigonometric Functions522 Questions
Exam 5: Analytic Trigonometry313 Questions
Exam 6: Applications of Trigonometry333 Questions
Exam 7: Systems and Matrices354 Questions
Exam 8: Analytic Geometry in Two and Three Dimensions167 Questions
Exam 9: Discrete Mathematics154 Questions
Exam 10: Statistics and Probability147 Questions
Exam 11: An Introduction to Calculus: Limits, Derivatives, and Integrals167 Questions
Exam 12: Prerequisites382 Questions
Select questions type
Match the function with the correct table values.
-
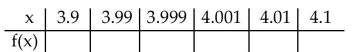
Free
(Multiple Choice)
5.0/5  (36)
(36)
Correct Answer:
B
Match the function with the correct table values.
-
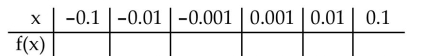
Free
(Multiple Choice)
4.8/5  (30)
(30)
Correct Answer:
A
Find the derivative of the function using the definition of derivative.
-
Free
(Multiple Choice)
4.9/5  (42)
(42)
Correct Answer:
B
Find the limit of the function by using direct substitution.
-
(Multiple Choice)
4.8/5  (39)
(39)
Use NINT on a calculator to find the numerical integral of the function over the specified interval.
-
(Multiple Choice)
5.0/5  (27)
(27)
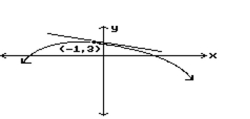
Estimate the slope of the tangent line at the indicated point.
-
(Multiple Choice)
4.9/5  (31)
(31)
Solve the problem.
-The position of an object at time is given by . Find the instantaneous velocity at the indicated value of . at
(Multiple Choice)
4.7/5  (47)
(47)
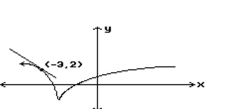
Estimate the slope of the tangent line at the indicated point.
-
(Multiple Choice)
4.8/5  (39)
(39)
Use the given graph to determine the limit, if it exists.
-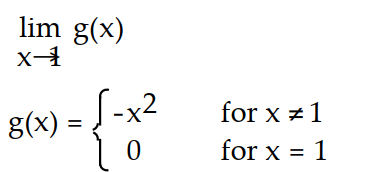
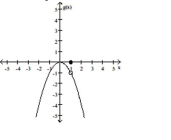
(Multiple Choice)
4.9/5  (28)
(28)
Solve the problem.
-Estimate the "RRAM" area under the graph of the function above the -axis and under the graph of the function from to . Use 5 subintervals.
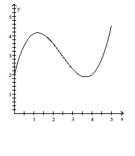
(Multiple Choice)
4.9/5  (28)
(28)
Use a graph of the function to find the derivative of the function at the given point, if it exists.
- at
(Multiple Choice)
4.9/5  (28)
(28)
Find the limit of the function by using direct substitution.
-
(Multiple Choice)
4.8/5  (25)
(25)
Use NINT on a calculator to find the numerical integral of the function over the specified interval.
-
(Multiple Choice)
4.8/5  (42)
(42)
Use NINT on a calculator to find the numerical integral of the function over the specified interval.
-
Round to three decimal places.
(Multiple Choice)
4.9/5  (30)
(30)
Showing 1 - 20 of 167
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)