Exam 5: Analytic Trigonometry
Exam 1: Functions and Graphs362 Questions
Exam 2: Polynomial, Power, and Rational Functions494 Questions
Exam 3: Exponential, Logistic, and Logarithmic Functions350 Questions
Exam 4: Trigonometric Functions522 Questions
Exam 5: Analytic Trigonometry313 Questions
Exam 6: Applications of Trigonometry333 Questions
Exam 7: Systems and Matrices354 Questions
Exam 8: Analytic Geometry in Two and Three Dimensions167 Questions
Exam 9: Discrete Mathematics154 Questions
Exam 10: Statistics and Probability147 Questions
Exam 11: An Introduction to Calculus: Limits, Derivatives, and Integrals167 Questions
Exam 12: Prerequisites382 Questions
Select questions type
Use the fundamental identities to find the value of the trigonometric function.
-Find if and
Free
(Multiple Choice)
4.8/5  (27)
(27)
Correct Answer:
B
Write the expression as the sine, cosine, or tangent of an angle.
-
Free
(Multiple Choice)
4.9/5  (38)
(38)
Correct Answer:
A
Complete the identity.
-The expression
is to be the left hand side of an equation that is an identity. Which one of the following four expressions can be used as the right hand side of the equation to complete the identity?
(Multiple Choice)
4.7/5  (27)
(27)
Use the fundamental identities to find the value of the trigonometric function.
-Find if and
(Multiple Choice)
4.9/5  (32)
(32)
Two triangles can be formed using the given measurements. Solve both triangles.
-
(Multiple Choice)
4.8/5  (32)
(32)
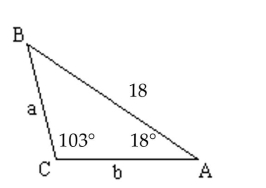
The given measurements may or may not determine a triangle. If not, then state that no triangle is formed. If a triangle is
formed, then use the Law of Sines to solve the triangle, if it is possible, or state that the Law of Sines cannot be used.
-
(Multiple Choice)
4.8/5  (33)
(33)
The given measurements may or may not determine a triangle. If not, then state that no triangle is formed. If a triangle is
formed, then use the Law of Sines to solve the triangle, if it is possible, or state that the Law of Sines cannot be used.
-
(Multiple Choice)
4.9/5  (30)
(30)
Showing 1 - 20 of 313
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)