Exam 3: Exponential, Logistic, and Logarithmic Functions
Exam 1: Functions and Graphs362 Questions
Exam 2: Polynomial, Power, and Rational Functions494 Questions
Exam 3: Exponential, Logistic, and Logarithmic Functions350 Questions
Exam 4: Trigonometric Functions522 Questions
Exam 5: Analytic Trigonometry313 Questions
Exam 6: Applications of Trigonometry333 Questions
Exam 7: Systems and Matrices354 Questions
Exam 8: Analytic Geometry in Two and Three Dimensions167 Questions
Exam 9: Discrete Mathematics154 Questions
Exam 10: Statistics and Probability147 Questions
Exam 11: An Introduction to Calculus: Limits, Derivatives, and Integrals167 Questions
Exam 12: Prerequisites382 Questions
Select questions type
Find the following using a calculator. Round to four decimal places.
-
Free
(Multiple Choice)
4.9/5  (35)
(35)
Correct Answer:
D
Graph the function and analyze it for domain, range, continuity, increasing or decreasing behavior, symmetry,
boundedness, extrema, asymptotes, and end behavior.
-
Free
(Essay)
4.7/5  (27)
(27)
Correct Answer:
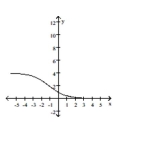 The domain is all real numbers, and the range is . The function is continuous and decreasing on its domain. The graph is symmetric about , but neither even nor odd. It is bounded below and above. There are no local extrema. The horizontal asymptotes are and . The end behavior is described by and .
The domain is all real numbers, and the range is . The function is continuous and decreasing on its domain. The graph is symmetric about , but neither even nor odd. It is bounded below and above. There are no local extrema. The horizontal asymptotes are and . The end behavior is described by and .
Find the exact solution to the equation.
-
Free
(Multiple Choice)
4.8/5  (47)
(47)
Correct Answer:
B
Graph the function. Describe its position relative to the graph of the indicated basic function.
-
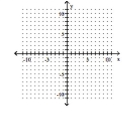
(Multiple Choice)
4.7/5  (38)
(38)
Find the following using a calculator. Round to four decimal places.
-
(Multiple Choice)
4.8/5  (34)
(34)
Graph the function. Describe its position relative to the graph of the indicated basic function.
-
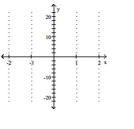
(Multiple Choice)
4.9/5  (38)
(38)
Determine a formula for the exponential function.
-The indicated point is . Which of the following is the correct equation of the function?
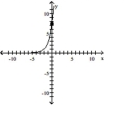
(Multiple Choice)
4.9/5  (37)
(37)
Solve the problem.
-The population of wolves in a state park after years is modeled by the function . What is the maximum number of wolves possible in the park?
(Multiple Choice)
4.9/5  (46)
(46)
Decide whether the function is an exponential growth or exponential decay function and find the constant percentage
rate of growth or decay.
-
(Multiple Choice)
4.8/5  (31)
(31)
Solve the problem.
-A $95,000 mortgage for 30 years at 11% APR requires monthly payments of $904.71. Suppose you decided to make monthly payments of $1,100. How much do you save with the greater payments compared to the original
Plan?
(Multiple Choice)
4.9/5  (35)
(35)
Solve the problem.
-Matthew obtains a 25-year $140,000 house loan with an APR of 8.88%. What is his monthly payment?
(Multiple Choice)
4.9/5  (30)
(30)
Assuming all variables are positive, use properties of logarithms to write the expression as a sum or difference of
logarithms or multiples of logarithms.
-
(Multiple Choice)
4.9/5  (25)
(25)
Solve the problem.
-Suppose the algae growth in Black Oak Lake increased from 100 cells per milliliter to approximately cells per milliliter in a 6-day period. The specific growth rate is defined by , where is the algae concentration at time and is the algae concentration at time . In this situation, what is the specific growth rate of algae? Round your results to the nearest hundredth.
(Multiple Choice)
4.9/5  (25)
(25)
Find the amount accumulated after investing a principal P for t years at an interest rate r.
-P = $14,000, t = 14, r = 8%, compounded semiannually (k = 2)
(Multiple Choice)
4.8/5  (32)
(32)
Graph the function. Describe its position relative to the graph of the indicated basic function.
-
(Multiple Choice)
4.8/5  (37)
(37)
Showing 1 - 20 of 350
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)