Exam 7: Systems and Matrices
Exam 1: Functions and Graphs362 Questions
Exam 2: Polynomial, Power, and Rational Functions494 Questions
Exam 3: Exponential, Logistic, and Logarithmic Functions350 Questions
Exam 4: Trigonometric Functions522 Questions
Exam 5: Analytic Trigonometry313 Questions
Exam 6: Applications of Trigonometry333 Questions
Exam 7: Systems and Matrices354 Questions
Exam 8: Analytic Geometry in Two and Three Dimensions167 Questions
Exam 9: Discrete Mathematics154 Questions
Exam 10: Statistics and Probability147 Questions
Exam 11: An Introduction to Calculus: Limits, Derivatives, and Integrals167 Questions
Exam 12: Prerequisites382 Questions
Select questions type
Determine which elementary row operation(s) applied to the first matrix will yield the second matrix.
-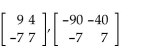
Free
(Essay)
4.8/5  (44)
(44)
Correct Answer:
(-10)R1
Write the augmented matrix for the system.
-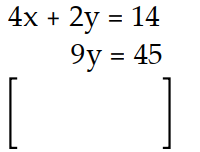
Free
(Multiple Choice)
4.9/5  (46)
(46)
Correct Answer:
C
Find a row echelon form or a reduced row echelon form, as indicated, for the given matrix.
-Find a reduced row echelon form for the matrix. 
(Essay)
4.9/5  (29)
(29)
Find the inverse of A if it has one, or state that the inverse does not exist.
-
(Multiple Choice)
4.8/5  (41)
(41)
Solve the problem.
-An airline with two types of airplanes, and , has contracted with a tour group to provide transportation for a minimum of 400 first class, 750 tourist class, and 1500 economy class passengers. For a certain trip, airplane costs to operate and can accommodate 20 first class, 50 tourist class, and 110 economy class passengers. Airplane costs to operate and can accommodate 18 first class, 30 tourist class, and 44 economy class passengers. How many of each type of airplane should be used in order to minimize the operating cost?
(Multiple Choice)
4.8/5  (29)
(29)
Graph the system of inequalities. Shade the region that represents the solution set.
- y \leq x+y >-3
(Multiple Choice)
4.9/5  (35)
(35)
Solve the problem.
-A certain area of forest is populated by two species of animals, which scientists refer to as A and B for simplicity. The forest supplies two kinds of food, referred to as and . For one year, species A requires units of and units of . Species requires units of and units of . The forest can normally supply at most 938 units of and 492 units of per year. What is the maximum total number of these animals that the forest can support?
(Multiple Choice)
4.8/5  (28)
(28)
Use Gaussian elimination to solve the system of equations.
-x + 4y + 5z = 9 4y + 2z = -10
Z = 5
(Multiple Choice)
4.8/5  (38)
(38)
Consider the equation 5(-3 - x) + x = 14x - 5(3 - x). Now consider the following system of equations solvable by the
substitution method:
y = 5(-3 - x) + x
y = 14x - 5(3 - x).
Explain the connections that exist between the single equation and the system of two equations.
(Essay)
4.8/5  (34)
(34)
Use Gaussian elimination to solve the system of equations.
- x+y+z=2 x-y+5z=-22 2x+y+z=7
(Multiple Choice)
4.8/5  (42)
(42)
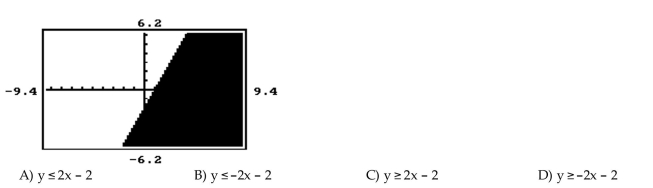
Determine which inequality matches the graph.
-
(Not Answered)
This question doesn't have any answer yet
Answer the question.
-Find , and so that the graph of the equation passes through the points , and .
(Multiple Choice)
4.8/5  (38)
(38)
Showing 1 - 20 of 354
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)