Exam 8: Confidence Interval Estimation

A major department store chain is interested in estimating the mean amount its credit card customers spent on their first visit to the chain's new store in the mall. Fifteen credit card accounts were randomly sampled and analyzed with the following results: 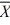=$50.50 and S = 20. Construct a 95% confidence interval for the mean amount its credit card customers spent on their first visit to the chain's new store in the mall assuming that the amount spent follows a normal distribution.

An economist is interested in studying the incomes of consumers in a particular country. The population standard deviation is known to be $1,000. A random sample of 50 individuals resulted in a mean income of $15,000. What is the width of the 90% confidence interval?

The difference between the sample proportion and the population proportion is called the sampling error.

TABLE 8-2 A quality control engineer is interested in the mean length of sheet insulation being cut automatically by machine. The desired mean length of the insulation is 12 feet. It is known that the standard deviation in the cutting length is 0.15 feet. A sample of 70 cut sheets yields a mean length of 12.14 feet. This sample will be used to obtain a 99% confidence interval for the mean length cut by machine. -Referring to Table 8-2, the confidence interval indicates that the machine is not working properly.

TABLE 8-6 After an extensive advertising campaign, the manager of a company wants to estimate the proportion of potential customers that recognize a new product. She samples 120 potential consumers and finds that 54 recognize this product. She uses this sample information to obtain a 95% confidence interval that goes from 0.36 to 0.54. -Referring to Table 8-6, 95% of the time, the proportion of people that recognize the product will fall between 0.36 and 0.54.

TABLE 8-7 A hotel chain wants to estimate the mean number of rooms rented daily in a given month. The population of rooms rented daily is assumed to be normally distributed for each month with a standard deviation of 24 rooms. During February, a sample of 25 days has a sample mean of 37 rooms. -Referring to Table 8-7, it is possible that the 99% confidence interval calculated from the data will not contain the population mean number of rooms rented daily in a given month.

A sample of 100 fuses from a very large shipment is found to have 10 that are defective. The 95% confidence interval would indicate that, for this shipment, the proportion of defective fuses is between 0 and 0.28.

TABLE 8-7 A hotel chain wants to estimate the mean number of rooms rented daily in a given month. The population of rooms rented daily is assumed to be normally distributed for each month with a standard deviation of 24 rooms. During February, a sample of 25 days has a sample mean of 37 rooms. -Referring to Table 8-7, the parameter of interest is the mean number of rooms rented daily in a given month.

TABLE 8-6 After an extensive advertising campaign, the manager of a company wants to estimate the proportion of potential customers that recognize a new product. She samples 120 potential consumers and finds that 54 recognize this product. She uses this sample information to obtain a 95% confidence interval that goes from 0.36 to 0.54. -The head of a computer science department is interested in estimating the proportion of students entering the department who will choose the new computer engineering option. A preliminary sample indicates that the proportion will be around 0.25. Therefore, what size sample should the department head take if she wants to be 95% confident that the estimate is within 0.10 of the true proportion?

TABLE 8-10 A university wanted to find out the percentage of students who felt comfortable reporting cheating by their fellow students. A survey of 2,800 students was conducted and the students were asked if they felt comfortable reporting cheating by their fellow students. The results were 1,344 answered "yes" and 1,456 answered "no". -Referring to Table 8-10, the parameter of interest is the proportion of the student population who feel comfortable reporting cheating by their fellow students.

TABLE 8-12 A poll was conducted by the marketing department of a video game company to determine the popularity of a new game that was targeted to be launched in three months. Telephone interviews with 1,500 young adults were conducted which revealed that 49% said they would purchase the new game. The margin of error was ±3 percentage points. -Referring to Table 8-12, what is the needed sample size to obtain a 95% confidence interval estimate of the percentage of the targeted young adults who will purchase the new game by allowing the same level of margin of error?

Holding the sample size fixed, increasing the level of confidence in a confidence interval will necessarily lead to a wider confidence interval.

A 99% confidence interval estimate can be interpreted to mean that

TABLE 8-1 The managers of a company are worried about the morale of their employees. In order to determine if a problem in this area exists, they decide to evaluate the attitudes of their employees with a standardized test. They select the Fortunato test of job satisfaction, which has a known standard deviation of 24 points. -Referring to Table 8-1, they should sample ________ employees if they want to estimate the mean score of the employees within 5 points with 90% confidence.

A prison official wants to estimate the proportion of cases of recidivism. Examining the records of 250 convicts, the official determines that there are 65 cases of recidivism. A confidence interval will be obtained for the proportion of cases of recidivism. Part of this calculation includes the estimated standard error of the sample proportion. For this sample, the estimated standard error is ________.

TABLE 8-4 The actual voltages of power packs labeled as 12 volts are as follows: 11.77, 11.90, 11.64, 11.84, 12.13, 11.99, and 11.77. -Referring to Table 8-4, it is possible that the 99% confidence interval calculated from the data will not contain the mean voltage for the sample.

TABLE 8-2 A quality control engineer is interested in the mean length of sheet insulation being cut automatically by machine. The desired mean length of the insulation is 12 feet. It is known that the standard deviation in the cutting length is 0.15 feet. A sample of 70 cut sheets yields a mean length of 12.14 feet. This sample will be used to obtain a 99% confidence interval for the mean length cut by machine. -Referring to Table 8-2, suppose the engineer had decided to estimate the mean length to within 0.03 with 99% confidence. Then the sample size would be ________.

The width of a confidence interval equals twice the sampling error.

TABLE 8-6 After an extensive advertising campaign, the manager of a company wants to estimate the proportion of potential customers that recognize a new product. She samples 120 potential consumers and finds that 54 recognize this product. She uses this sample information to obtain a 95% confidence interval that goes from 0.36 to 0.54. -Referring to Table 8-6, this interval requires the assumption that the distribution of the number of people recognizing the product has a normal distribution.

TABLE 8-8 The president of a university would like to estimate the proportion of the student population that owns a personal computer. In a sample of 500 students, 417 own a personal computer. -Referring to Table 8-8, a confidence interval estimate of the population proportion would only be valid if the distribution of the number of students who own a personal computer is normal.