Exam 8: Confidence Interval Estimation

In the construction of confidence intervals, if all other quantities are unchanged, an increase in the sample size will lead to a ________ interval.

TABLE 8-4 The actual voltages of power packs labeled as 12 volts are as follows: 11.77, 11.90, 11.64, 11.84, 12.13, 11.99, and 11.77. -Referring to Table 8-4, a 99% confidence interval for the mean voltage of the power packs is from ________ to ________.

The confidence interval obtained will always correctly estimate the population parameter.

If you were constructing a 99% confidence interval of the population mean based on a sample of n = 25 where the standard deviation of the sample S = 0.05, the critical value of t will be ________.

For a t distribution with 12 degrees of freedom, the area between -2.6810 and 2.1788 is 0.980.

TABLE 8-4 The actual voltages of power packs labeled as 12 volts are as follows: 11.77, 11.90, 11.64, 11.84, 12.13, 11.99, and 11.77. -Referring to Table 8-4, a 95% confidence interval for the mean voltage of the power pack is wider than a 99% confidence interval.

TABLE 8-11 A sales and marketing management magazine conducted a survey on salespeople cheating on their expense reports and other unethical conduct. In the survey on 200 managers, 58% of the managers have caught salespeople cheating on an expense report, 50% have caught salespeople working a second job on company time, 22% have caught salespeople listing a "strip bar" as a restaurant on an expense report, and 19% have caught salespeople giving a kickback to a customer. -Referring to Table 8-11, the sampling error of a 95% confidence interval estimate of the population proportion of managers who have caught salespeople cheating on an expense report is ________.

TABLE 8-7 A hotel chain wants to estimate the mean number of rooms rented daily in a given month. The population of rooms rented daily is assumed to be normally distributed for each month with a standard deviation of 24 rooms. During February, a sample of 25 days has a sample mean of 37 rooms. -Referring to Table 8-7, the sampling error of a 99% confidence interval for the mean number of rooms rented daily in a given month is ________.

TABLE 8-6 After an extensive advertising campaign, the manager of a company wants to estimate the proportion of potential customers that recognize a new product. She samples 120 potential consumers and finds that 54 recognize this product. She uses this sample information to obtain a 95% confidence interval that goes from 0.36 to 0.54. -Referring to Table 8-6, this interval requires the use of the t distribution to obtain the confidence coefficient.

TABLE 8-3 To become an actuary, it is necessary to pass a series of 10 exams, including the most important one, an exam in probability and statistics. An insurance company wants to estimate the mean score on this exam for actuarial students who have enrolled in a special study program. They take a sample of 8 actuarial students in this program and determine that their scores are: 2, 5, 8, 8, 7, 6, 5, and 7. This sample will be used to calculate a 90% confidence interval for the mean score for actuarial students in the special study program. -Referring to Table 8-3, the mean of the sample is ________, while the standard deviation of the sample is ________.

TABLE 8-7 A hotel chain wants to estimate the mean number of rooms rented daily in a given month. The population of rooms rented daily is assumed to be normally distributed for each month with a standard deviation of 24 rooms. During February, a sample of 25 days has a sample mean of 37 rooms. -Referring to Table 8-7, we are 99% confident that between 24.64% and 49.36% of the rooms will be rented daily in a given month.

An economist is interested in studying the incomes of consumers in a particular country. The population standard deviation is known to be $1,000. A random sample of 50 individuals resulted in a mean income of $15,000. What is the upper end point in a 99% confidence interval for the average income?

As an aid to the establishment of personnel requirements, the director of a hospital wishes to estimate the mean number of people who are admitted to the emergency room during a 24-hour period. The director randomly selects 64 different 24-hour periods and determines the number of admissions for each. For this sample, 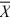= 19.8 and S² = 25. Estimate the mean number of admissions per 24-hour period with a 95% confidence interval.

TABLE 8-10 A university wanted to find out the percentage of students who felt comfortable reporting cheating by their fellow students. A survey of 2,800 students was conducted and the students were asked if they felt comfortable reporting cheating by their fellow students. The results were 1,344 answered "yes" and 1,456 answered "no". -Referring to Table 8-10, a 95% confidence interval for the proportion of the student population who feel comfortable reporting cheating by their fellow students is narrower than a 99% confidence interval.

A race car driver tested his car for time from 0 to 60 mph, and for 20 tests obtained a mean of 4.85 seconds with a standard deviation of 1.47 seconds. A 95% confidence interval for the 0 to 60 mean time is 4.52 seconds to 5.18 seconds.

TABLE 8-5 A sample of salary offers (in thousands of dollars) given to management majors is: 48, 51, 46, 52, 47, 48, 47, 50, 51, and 59. Using this data to obtain a 95% confidence interval resulted in an interval from 47.19 to 52.61. -Referring to Table 8-5, 95% of the salary offers are between 47.19 and 52.61.

TABLE 8-10 A university wanted to find out the percentage of students who felt comfortable reporting cheating by their fellow students. A survey of 2,800 students was conducted and the students were asked if they felt comfortable reporting cheating by their fellow students. The results were 1,344 answered "yes" and 1,456 answered "no". -Referring to Table 8-10, a 90% confidence interval calculated from the same data would be narrower than a 99% confidence interval.

TABLE 8-6 After an extensive advertising campaign, the manager of a company wants to estimate the proportion of potential customers that recognize a new product. She samples 120 potential consumers and finds that 54 recognize this product. She uses this sample information to obtain a 95% confidence interval that goes from 0.36 to 0.54. -Referring to Table 8-6, it is possible that the true proportion of people that recognize the product is between 0.36 and 0.54.

TABLE 8-5 A sample of salary offers (in thousands of dollars) given to management majors is: 48, 51, 46, 52, 47, 48, 47, 50, 51, and 59. Using this data to obtain a 95% confidence interval resulted in an interval from 47.19 to 52.61. -Referring to Table 8-5, a 99% confidence interval for the mean of the population from the same sample would be wider than 47.19 to 52.61.

A university system enrolling hundreds of thousands of students is considering a change in the way students pay for their education. Currently, the students pay $400 per credit hour. The university system administrators are contemplating charging each student a set fee of $7,000 per quarter, regardless of how many credit hours each takes. To see if this proposal would be economically feasible, the administrators would like to know how many credit hours, on the average, each student takes per quarter. A random sample of 250 students yields a mean of 14.1 credit hours per quarter and a standard deviation of 2.3 credit hours per quarter. Suppose the administration wanted to estimate the mean to within 0.1 hours at 95% reliability and assumed that the sample standard deviation provided a good estimate for the population standard deviation. How large a total sample would they need to take?