Exam 10: Analytic Geometry in Three Dimensions
Exam 1: Functions and Their Graphs118 Questions
Exam 2: Polynomial and Rational Functions120 Questions
Exam 3: Exponential and Logarithmic Functions120 Questions
Exam 4: Trigonometric Functions118 Questions
Exam 5: Analytic Trigonometry120 Questions
Exam 6: Additional Topics in Trigonometry120 Questions
Exam 7: Linear Systems and Matrices120 Questions
Exam 8: Sequences, Series, and Probability119 Questions
Exam 9: Topics in Analytic Geometry120 Questions
Exam 10: Analytic Geometry in Three Dimensions120 Questions
Exam 11: Limits and an Introduction to Calculus40 Questions
Exam 12: Review of Graphs, Equations, and Inequalities99 Questions
Select questions type
The weight of a crate is 200 newtons. Find the tension in each of the supporting cables shown in the figure. The coordinates of the points , and are given below the figure. Round to the nearest newton.
![The weight of a crate is 200 newtons. Find the tension in each of the supporting cables shown in the figure. The coordinates of the points A , B , C , and D are given below the figure. Round to the nearest newton. [Figure not necessarily to scale.] point A = ( 0,0 , - 180 ) , point B = ( 110,0,0 ) , point C = ( - 40,50,0 ) , point D = ( 0 , - 130,0 )](https://storage.examlex.com/TB8201/11ecdf2a_4bee_6e07_b402_3b2413191132_TB8201_11.jpg) [Figure not necessarily to scale.]
point , point , point , point
[Figure not necessarily to scale.]
point , point , point , point
(Multiple Choice)
4.9/5  (34)
(34)
The lights in an auditorium are 25-pound disks of radius 16 inches. Each disk is supported by three equally spaced 50-inch wires attached to the ceiling. Find the Tension in each wire. Round your answer to two decimals. 
(Multiple Choice)
4.7/5  (33)
(33)
Find the general form of the equation of the plane with the given characteristics. The plane passes through the points and and is perpendicular to the plane .
(Multiple Choice)
4.9/5  (27)
(27)
Find the general form of the equation of the plane passing through the three points. [Be sure to reduce the coefficients in your answer to lowest terms by dividing out any common factor.]
(Multiple Choice)
4.9/5  (34)
(34)
Find a set of symmetric equations of the line that passes through the points and .
(Multiple Choice)
5.0/5  (33)
(33)
Find the angle between the two planes in degrees. Round to a tenth of a degree.
x+2y+6z=0 -4x-y-3z=0
(Multiple Choice)
4.9/5  (35)
(35)
Find a set of parametric equations for the line through the point and parallel to the specified line. Show all your work. x=-7-7t (-8,-4,3), parallel to y=2-8t z=-4+9t
(Essay)
4.8/5  (31)
(31)
Find the area of the parallelogram formed by the points , , and .
(Multiple Choice)
4.8/5  (29)
(29)
The lights in an auditorium are 25-pound disks of radius 16 inches. Each disk is supported by three equally spaced 60-inch wires attached to the ceiling. Find the Tension in each wire. Round your answer to two decimals. 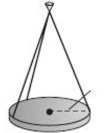
(Multiple Choice)
4.7/5  (34)
(34)
Find the angle between the vectors and . Express your answer in degrees and round to the nearest tenth of a degree.
(Multiple Choice)
4.9/5  (44)
(44)
Use the scalar triple product to find the volume of the parallelepiped having adjacent edges , and .
(Multiple Choice)
4.8/5  (28)
(28)
The lights in an auditorium are 30-pound disks of radius 24 inches. Each disk is supported by three equally spaced 45 -inch wires attached to the ceiling. Find the tension in each wire. Round your answer to two decimals.
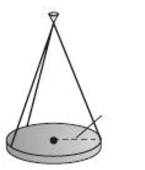
(Multiple Choice)
4.9/5  (27)
(27)
Find the magnitude of the vector described below.
Initial point:
Terminal point:
(Multiple Choice)
4.9/5  (35)
(35)
Showing 101 - 120 of 120
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)