Exam 2: Limits and Derivatives
Exam 1: Functions and Models112 Questions
Exam 2: Limits and Derivatives76 Questions
Exam 3: Differentiation Rules75 Questions
Exam 4: Applications of Differentiation77 Questions
Exam 5: Integrals60 Questions
Exam 6: Applications of Integration78 Questions
Exam 7: Techniques of Integration79 Questions
Exam 8: Further Applications of Integration59 Questions
Exam 9: Differential Equations60 Questions
Exam 10: Parametric Equations and Polar Coordinates60 Questions
Exam 11: Infinite Sequences and Series60 Questions
Exam 12: Vectors and the Geometry of Space54 Questions
Exam 13: Vector Functions58 Questions
Exam 14: Partial Derivatives39 Questions
Exam 15: Multiple Integrals60 Questions
Exam 16: Vector Calculus59 Questions
Exam 17: Second-Order Differential Equations60 Questions
Select questions type
A plane flying horizontally at an altitude of and a speed of passes directly over a radar station. Find the rate at which the distance from the plane to the station is increasing when it is away from the station.
Free
(Multiple Choice)
4.9/5  (40)
(40)
Correct Answer:
A
Find the points on the curve where the tangent is horizontal.
Free
(Multiple Choice)
4.9/5  (34)
(34)
Correct Answer:
A
In an adiabatic process (one in which no heat transfer takes place), the pressure P and volume V of an ideal gas such as oxygen satisfy the equation where is a constant. Suppose that at a certain instant of time, the volume of the gas is , the pressure is , and the pressure is decreasing at the rate of . Find the rate at which the volume is changing.
(Multiple Choice)
4.8/5  (39)
(39)
Suppose the total cost in maunufacturing units of a certain product is dollars.
a. What does measure? Give units.
b. What can you say about the sign of ?
c. Given that , estimate the additional cost in producing the 3001 st unit of the product.
(Essay)
4.8/5  (38)
(38)
Find the instantaneous rate of change of the function when .
(Multiple Choice)
4.9/5  (31)
(31)
Determine the values of for which the given linear approximation is accurate to within at .
(Multiple Choice)
4.9/5  (36)
(36)
Let .
a. Sketch the graph of .
b. For what values of is differentiable?
c. Find a formula for .
(Essay)
4.8/5  (35)
(35)
Find an equation of the tangent line to the given curve at the indicated point.
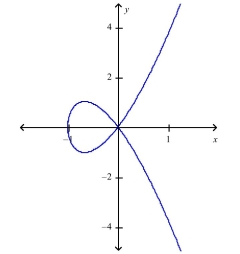
(Essay)
4.9/5  (33)
(33)
The mass of the part of a metal rod that lies between its left end and a point x meters to the right is Find the linear density when is .
(Multiple Choice)
4.9/5  (38)
(38)
A point moves along the curve . When the point is at , its -coordinate is increasing at the rate of 3 units per second. How fast is its -coordinate changing at that instant of time?
(Multiple Choice)
4.8/5  (42)
(42)
Water flows from a tank of constant cross-sectional area through an orifice of constant cross-sectional area located at the bottom of the tank. Initially, the height of the water in the tank was , and sec later it was given by the equation
How fast was the height of the water decreasing when its height was ?
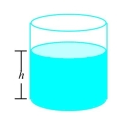
(Multiple Choice)
4.9/5  (36)
(36)
Find the differential of the function at the indicated number.
(Multiple Choice)
4.9/5  (35)
(35)
In calm waters, the oil spilling from the ruptured hull of a grounded tanker spreads in all directions. Assuming that the polluted area is circular, determine how fast the area is increasing when the radius of the circle is and is increasing at the rate of . Round to the nearest tenth if necessary.
(Essay)
4.7/5  (30)
(30)
Showing 1 - 20 of 76
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)