Exam 15: Multiple Integrals
Exam 1: Functions and Models112 Questions
Exam 2: Limits and Derivatives76 Questions
Exam 3: Differentiation Rules75 Questions
Exam 4: Applications of Differentiation77 Questions
Exam 5: Integrals60 Questions
Exam 6: Applications of Integration78 Questions
Exam 7: Techniques of Integration79 Questions
Exam 8: Further Applications of Integration59 Questions
Exam 9: Differential Equations60 Questions
Exam 10: Parametric Equations and Polar Coordinates60 Questions
Exam 11: Infinite Sequences and Series60 Questions
Exam 12: Vectors and the Geometry of Space54 Questions
Exam 13: Vector Functions58 Questions
Exam 14: Partial Derivatives39 Questions
Exam 15: Multiple Integrals60 Questions
Exam 16: Vector Calculus59 Questions
Exam 17: Second-Order Differential Equations60 Questions
Select questions type
Find the volume of the solid bounded in the first octanat bounded by the cylinder and the planes .
Free
(Short Answer)
4.8/5  (34)
(34)
Correct Answer:
18
Use spherical coordinates. Evaluate , where is the ball with center the origin and radius 5 .
(Multiple Choice)
4.8/5  (41)
(41)
Find the mass of the lamina that occupies the region and has the given density function. Round your answer to two decimal places.
(Short Answer)
4.8/5  (27)
(27)
Use polar coordinates to find the volume of the solid inside the cylinder and the ellipsoid .
(Multiple Choice)
4.8/5  (33)
(33)
Evaluate the iterated integral by converting to polar coordinates.Round the answer to two decimal places.
(Multiple Choice)
4.8/5  (27)
(27)
Determine whether to use polar coordinates or rectangular coordinates to evaluate the integral , where is a continuous function. Then write an expression for the (iterated) integral.
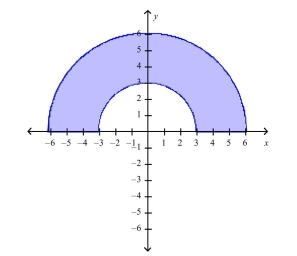
(Essay)
4.9/5  (38)
(38)
Find the area of the surface where is the part of the sphere that lies inside the cylinder .
(Short Answer)
4.7/5  (34)
(34)
Evaluate the integral , where is the annular region bounded by the circles and , by changing to polar coordinates.
(Short Answer)
4.8/5  (32)
(32)
Use cylindrical coordinates to evaluate , where is the solid bounded by the cylinder and the planes and .
(Multiple Choice)
4.8/5  (32)
(32)
Use spherical coordinates to evaluate , where is the ball .
(Multiple Choice)
4.7/5  (30)
(30)
Find the area of the surface where is the part of the plane that lies above the triangular region with vertices , and .
(Short Answer)
4.8/5  (31)
(31)
Evaluate the integral where and with respect to , and , in that order.
(Multiple Choice)
4.8/5  (29)
(29)
Find the mass and the center of mass of the lamina occupying the region , where is the region bounded by the graphs of , and , and having the mass density
(Short Answer)
4.8/5  (34)
(34)
Use cylindrical coordinates to evaluate the triple integral
where is the solid that lies between the cylinders and above the -plane and below the plane .
(Multiple Choice)
4.9/5  (39)
(39)
Showing 1 - 20 of 60
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)