Exam 8: The Arbitrage-Free Valuation Framework
Exam 1: Fixed-Income Securities: Defining Elements28 Questions
Exam 2: Fixed-Income Markets: Issuance, Trading, and Funding31 Questions
Exam 3: Introduction to Fixed-Income Valuation44 Questions
Exam 4: Introduction to Asset-Backed Securities42 Questions
Exam 5: Understanding Fixed Income Risk and Return27 Questions
Exam 6: Fundamentals of Credit Analysis45 Questions
Exam 7: The Term Structure and Interest Rate Dynamics56 Questions
Exam 8: The Arbitrage-Free Valuation Framework17 Questions
Exam 9: Valuation and Analysis of Bonds With Embedded Options36 Questions
Exam 10: Credit Analysis Models30 Questions
Exam 11: Credit Default Swaps15 Questions
Exam 12: Overview of Fixed-Income Portfolio Management12 Questions
Exam 13: Liability-Driven and Index-Based Strategies26 Questions
Exam 14: Yield Curve Strategies32 Questions
Exam 15: Fixed-Income Active Management: Credit Strategies15 Questions
Select questions type
The following information relates to Questions
Meredith alvarez is a junior fixed-income analyst with Canzim asset Management. her su-pervisor, Stephanie hartson, asks alvarez to review the asset price and payoff data shown in exhibit 1 to determine whether an arbitrage opportunity exists.exhibit 1 Price and Payoffs for two risk-Free assets
Asset Price Today Payoff in One Year Asset A \ 500 \ 525 Asset B \ 1,000 \ 1,100
hartson also shows alvarez data for a bond that trades in three different markets in the same currency. These data appear in exhibit 2.
exhibit 2 2% Coupon, Five-Year Maturity, annual-Pay bond
New York Hong Kong Mumbai Yield to Maturity 1.9\% 2.3\% 2.0\%
hartson asks alvarez to value two bonds (bond C and bond D) using the binomial tree in exhibit 3. exhibit 4 presents selected data for both bonds.
exhibit 3 binomial interest rate tree with Volatility = 25%
Time 0 Time 1 Time 2 2.7183\% 2.8853\% 1.500\% 1.6487\% 1.7500\% 1.0000\%
exhibit 4 Selected Data on annual-Pay bonds
Bond Maturity Coupon Rate Bond C 2 years 2.5\% Bond D 3 years 3.0\%
hartson tells alvarez that she and her peers have been debating various viewpoints regard-ing the conditions underlying binomial interest rate trees. The following statements were made in the course of the debate.
Statement 1: The only requirements needed to create a binomial interest rate tree are current benchmark interest rates and an assumption about interest rate volatility.
Statement 2: Potential interest rate volatility in a binomial interest rate tree can be es-timated using historical interest rate volatility or observed arket prices from interest rate derivatives.
Statement 3: a bond value derived from a binomial interest rate tree with a relatively
high volatility assumption will be different from the value calculated by discounting the bond's cash flows using current spot rates. based on data in exhibit 5, hartson asks alvarez to calibrate a binomial interest rate tree starting with the calculation of implied forward rates shown in exhibit 6.
exhibit 5 Selected Data for a binomial interest rate tree
Maturity Par Rate Spot Rate 1 2.5000\% 2.5000\% 2 3.5000\% 3.5177\%
exhibit 6 Calibration of binomial interest rate
Tree with Volatility =25\% Time 0 Time 1 5.8365\% 2.500\% Lower one-period forward rate
hartson mentions pathwise valuations as another method to value bonds using a binomial
interest rate tree. using the binomial interest rate tree in exhibit 3, alvarez calculates the pos-sible interest rate paths for bond D shown in exhibit 7.
exhibit 7 interest rate Paths for bond D
Path Time 0 Time 1 Time 2 1 1.500\% 2.8853\% 2.7183\% 2 1.500 2.8853 1.6487 3 1.500 1.7500 1.6487 4 1.500 1.7500 1.0000
before leaving for the day, hartson asks alvarez about the value of using the Monte Carlo method to simulate a large number of potential interest rate paths to value a bond. alvarez makes the following statements.
Statement 4: increasing the number of paths increases the estimate's statistical accuracy.
Statement 5: The bond value derived from aMonte Carlo simulation will be closer to the bond's true fundamental value.
-based on the data in exhibit 2, the most profitable arbitrage opportunity would be to buy the bond in:
Free
(Multiple Choice)
4.8/5  (32)
(32)
Correct Answer:
B
The following information relates to Questions
betty tatton is a fixed income analyst with the hedge fund Sailboat asset Management (SaM).SaM invests in a variety of global fixed-income strategies, including fixed-income arbitrage.tatton is responsible for pricing individual investments and analyzing market data to assess the opportunity for arbitrage. She uses two methods to value bonds:
Method 1: Discount each year's cash flow separately using the appropriate interest rate curve.
Method 2: build and use a binomial interest rate tree.
tatton compiles pricing data for a list of annual pay bonds (exhibit 1). each of the bonds will mature in two years, and tatton considers the bonds as being risk-free; both the one-year and two-year benchmark spot rates are 2%. tatton calculates the arbitrage-free prices and identifies an arbitrage opportunity to recommend to her team.exhibit 1 Market Data for Selected bonds
Asset Coupon Market Price Bond A 1\% 98.0584 Bond B 3\% 100.9641 Bond C 5\% 105.8247
next, tatton uses the benchmark yield curve provided in exhibit 2 to consider arbitrage opportunities of both option-free corporate bonds and corporate bonds with embedded op-tions. The benchmark bonds in exhibit 2 pay coupons annually, and the bonds are priced at par.exhibit 2 benchmark Par Curve
Maturity (years) Yield to Maturity (YTM) 1 3.0\% 2 4.0\% 3 5.0\% tatton then identifies three mispriced three-year annual-pay bonds and compiles data onthe bonds (see exhibit 3).
exhibit 3 Market Data of annual-Pay Corporate bonds Company Coupon Market Price Yield Embedded Option? Hutto-Barkley Inc. 3\% 94.9984 5.6\% No Luna y Estrellas Intl. 0\% 88.8996 4.0\% Yes Peaton Scorpio Motors 0\% 83.9619 6.0\% No
last, tatton identifies two mispriced Swiss bonds, ond x, a three-year bond, and bond Y, a five-year bond. both are annual-pay bonds with a coupon rate of 6%. to calculate the bonds' values, tatton devises the first three years of the interest rate lognormal tree presented in exhibit 4 using historical interest rate volatility data. tatton considers how these data would change if implied volatility, which is higher than historical volatility, were used instead.
exhibit 4 interest rate tree; Forward rates based on Swiss Market
 -based on exhibits 2 and 3 and using Method 1, the amount (in absolute terms) by which the hutto-barkley corporate bond is mispriced is closest to:
-based on exhibits 2 and 3 and using Method 1, the amount (in absolute terms) by which the hutto-barkley corporate bond is mispriced is closest to:
Free
(Multiple Choice)
4.8/5  (42)
(42)
Correct Answer:
C
The following information relates to Questions
Meredith alvarez is a junior fixed-income analyst with Canzim asset Management. her su-pervisor, Stephanie hartson, asks alvarez to review the asset price and payoff data shown in exhibit 1 to determine whether an arbitrage opportunity exists.exhibit 1 Price and Payoffs for two risk-Free assets
Asset Price Today Payoff in One Year Asset A \ 500 \ 525 Asset B \ 1,000 \ 1,100
hartson also shows alvarez data for a bond that trades in three different markets in the same currency. These data appear in exhibit 2.
exhibit 2 2% Coupon, Five-Year Maturity, annual-Pay bond
New York Hong Kong Mumbai Yield to Maturity 1.9\% 2.3\% 2.0\%
hartson asks alvarez to value two bonds (bond C and bond D) using the binomial tree in exhibit 3. exhibit 4 presents selected data for both bonds.
exhibit 3 binomial interest rate tree with Volatility = 25%
Time 0 Time 1 Time 2 2.7183\% 2.8853\% 1.500\% 1.6487\% 1.7500\% 1.0000\%
exhibit 4 Selected Data on annual-Pay bonds
Bond Maturity Coupon Rate Bond C 2 years 2.5\% Bond D 3 years 3.0\%
hartson tells alvarez that she and her peers have been debating various viewpoints regard-ing the conditions underlying binomial interest rate trees. The following statements were made in the course of the debate.
Statement 1: The only requirements needed to create a binomial interest rate tree are current benchmark interest rates and an assumption about interest rate volatility.
Statement 2: Potential interest rate volatility in a binomial interest rate tree can be es-timated using historical interest rate volatility or observed arket prices from interest rate derivatives.
Statement 3: a bond value derived from a binomial interest rate tree with a relatively
high volatility assumption will be different from the value calculated by discounting the bond's cash flows using current spot rates. based on data in exhibit 5, hartson asks alvarez to calibrate a binomial interest rate tree starting with the calculation of implied forward rates shown in exhibit 6.
exhibit 5 Selected Data for a binomial interest rate tree
Maturity Par Rate Spot Rate 1 2.5000\% 2.5000\% 2 3.5000\% 3.5177\%
exhibit 6 Calibration of binomial interest rate
Tree with Volatility =25\% Time 0 Time 1 5.8365\% 2.500\% Lower one-period forward rate
hartson mentions pathwise valuations as another method to value bonds using a binomial
interest rate tree. using the binomial interest rate tree in exhibit 3, alvarez calculates the pos-sible interest rate paths for bond D shown in exhibit 7.
exhibit 7 interest rate Paths for bond D
Path Time 0 Time 1 Time 2 1 1.500\% 2.8853\% 2.7183\% 2 1.500 2.8853 1.6487 3 1.500 1.7500 1.6487 4 1.500 1.7500 1.0000
before leaving for the day, hartson asks alvarez about the value of using the Monte Carlo method to simulate a large number of potential interest rate paths to value a bond. alvarez makes the following statements.
Statement 4: increasing the number of paths increases the estimate's statistical accuracy.
Statement 5: The bond value derived from aMonte Carlo simulation will be closer to the bond's true fundamental value.
-which of the statements regarding Monte Carlo simulation is correct?
Free
(Multiple Choice)
4.9/5  (33)
(33)
Correct Answer:
A
The following information relates to Questions 1-6
katrina black, portfolio manager at Coral bond Management, ltd., is conducting a training session with alex Sun, a junior analyst in the fixed income department. black wants to ex-plain to Sun the arbitrage-free valuation framework used by the firm. black presents Sun with exhibit 1, showing a fictitious bond being traded on three exchanges, and asks Sun to identify the arbitrage opportunity of the bond. Sun agrees to ignore transaction costs in his analysis.exhibit 1 Three-Year, €100 par, 3.00% Coupon, annual-Pay option-Free bond
Eurex NYSE Euronext Frankfurt Price 103.7956 103.7815 103.7565 black shows Sun some exhibits that were part of a recent presentation. exhibit 3 presents most of the data of a binomial lognormal interest rate tree fit to the yield curve shown in ex-hibit 2. exhibit 4 presents most of the data of the implied values for a four-year, option-free, annual-pay bond with a 2.5% coupon based on the information in exhibit 3.exhibit 2 Yield to Maturity Par rates for one-, two-, and Three-Year annual-Pay option-Free bonds
One-Year Two-Year Three-Year 1.25\% 1.50\% 1.70\% exhibit 3 binomial interest rate tree Fit to the Yield Curve (Volatility = 10%)
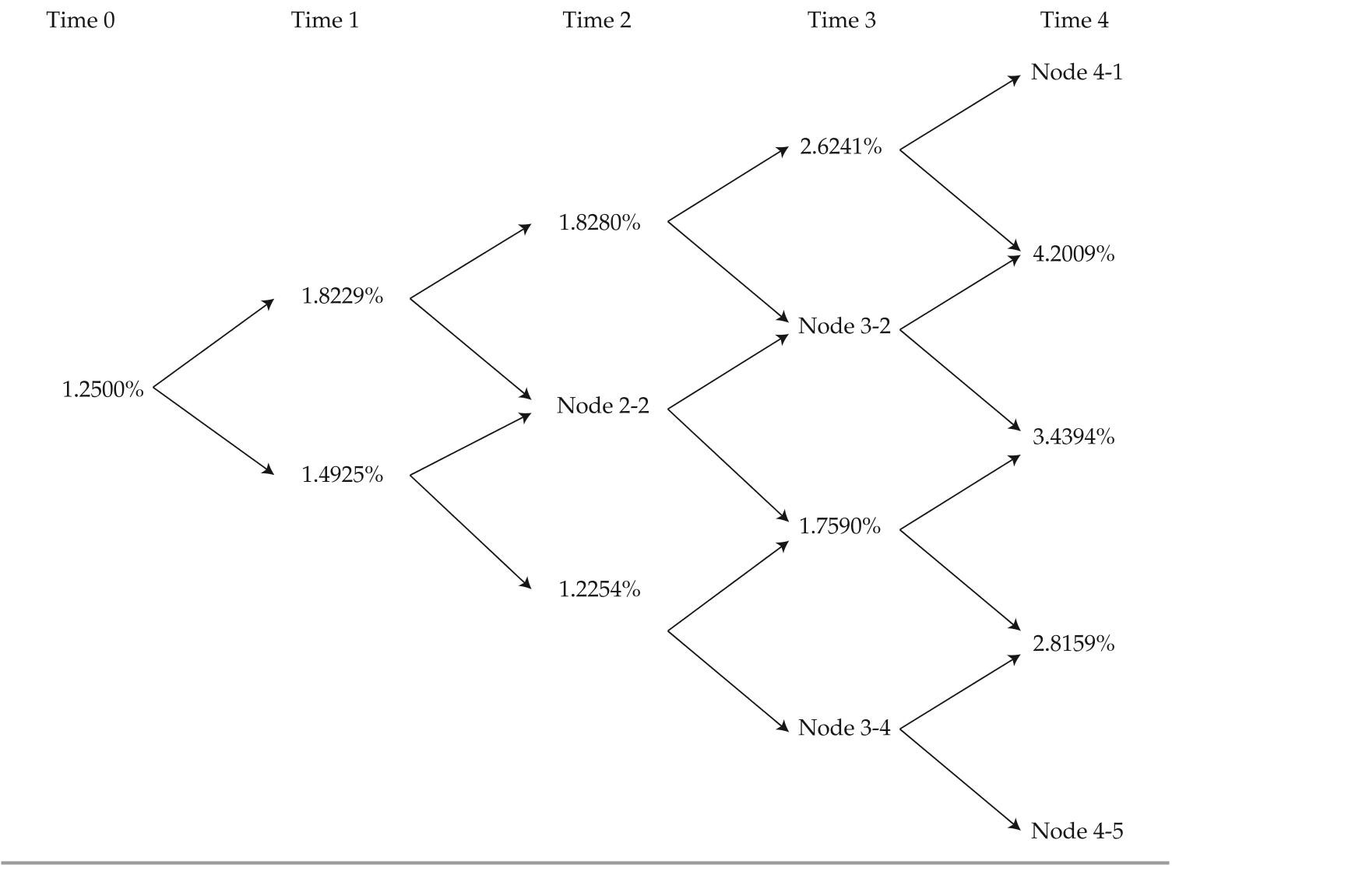 exhibit 4 implied Values (in euros) for a 2.5%, Four-Year, option-Free, annual-Pay bond based on exhibit 3
exhibit 4 implied Values (in euros) for a 2.5%, Four-Year, option-Free, annual-Pay bond based on exhibit 3
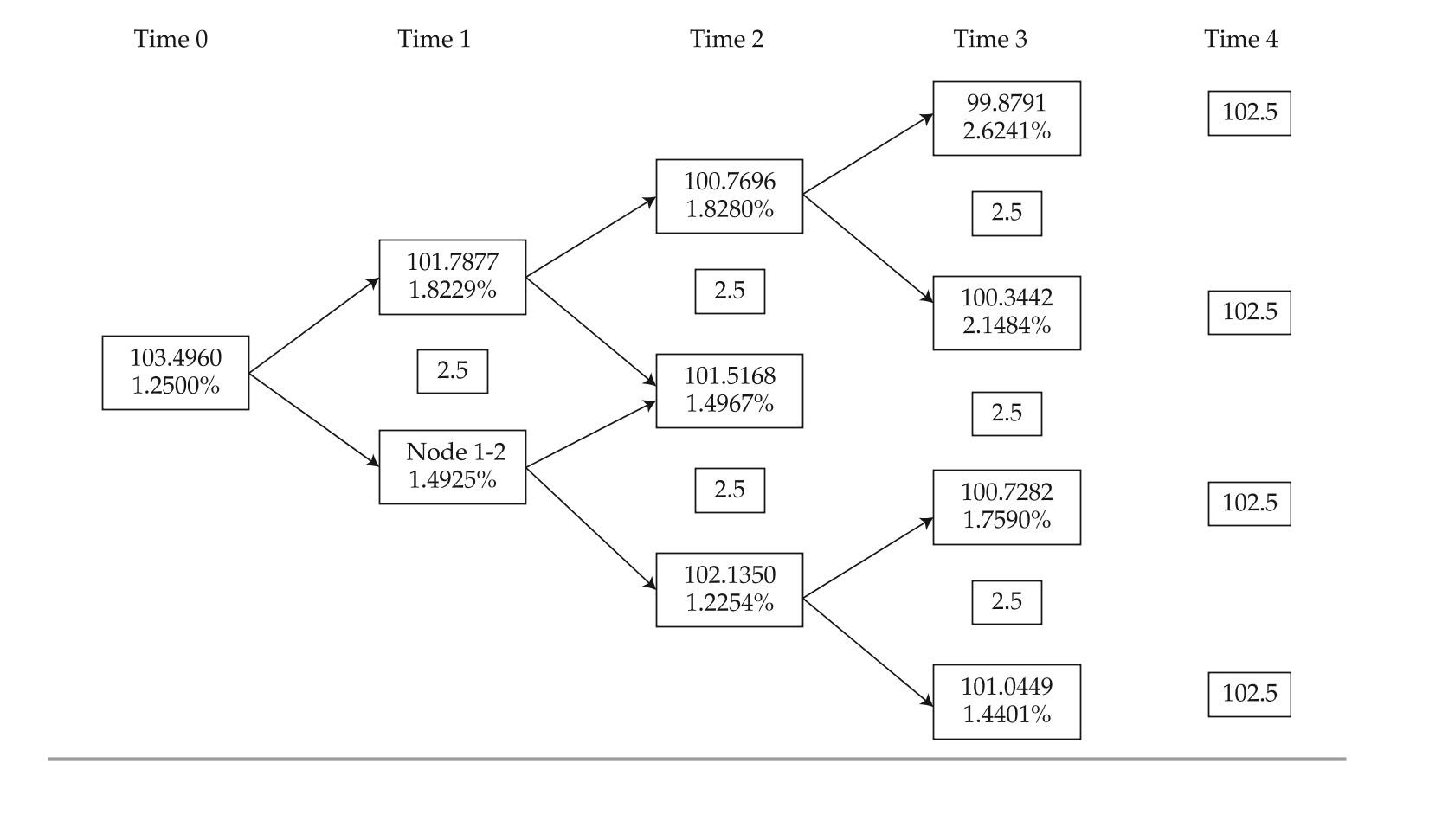 black asks about the missing data in exhibits 3 and 4 and directs Sun to complete the following tasks related to those exhibits:
task 1 test that the binomial interest tree has been properly calibrated to be arbitrage-free.
task 2 Develop a spreadsheet model to calculate pathwise valuations. to test the ac-curacy of the spreadsheet, use the data in exhibit 3 and calculate the value of the bond if it takes a path of lowest rates in Year 1 and Year 2 and the second lowest rate in Year 3.
task 3 identify a type of bond where the Monte Carlo calibration method should be used in place of the binomial interest rate method.
task 4 update exhibit 3 to reflect the current volatility, which is now 15%.
-based on exhibits 1 and 2, the exchange that reflects the arbitrage-free price of the bond is:
black asks about the missing data in exhibits 3 and 4 and directs Sun to complete the following tasks related to those exhibits:
task 1 test that the binomial interest tree has been properly calibrated to be arbitrage-free.
task 2 Develop a spreadsheet model to calculate pathwise valuations. to test the ac-curacy of the spreadsheet, use the data in exhibit 3 and calculate the value of the bond if it takes a path of lowest rates in Year 1 and Year 2 and the second lowest rate in Year 3.
task 3 identify a type of bond where the Monte Carlo calibration method should be used in place of the binomial interest rate method.
task 4 update exhibit 3 to reflect the current volatility, which is now 15%.
-based on exhibits 1 and 2, the exchange that reflects the arbitrage-free price of the bond is:
(Multiple Choice)
4.8/5  (29)
(29)
The following information relates to Questions 1-6
katrina black, portfolio manager at Coral bond Management, ltd., is conducting a training session with alex Sun, a junior analyst in the fixed income department. black wants to ex-plain to Sun the arbitrage-free valuation framework used by the firm. black presents Sun with exhibit 1, showing a fictitious bond being traded on three exchanges, and asks Sun to identify the arbitrage opportunity of the bond. Sun agrees to ignore transaction costs in his analysis.exhibit 1 Three-Year, €100 par, 3.00% Coupon, annual-Pay option-Free bond
Eurex NYSE Euronext Frankfurt Price 103.7956 103.7815 103.7565 black shows Sun some exhibits that were part of a recent presentation. exhibit 3 presents most of the data of a binomial lognormal interest rate tree fit to the yield curve shown in ex-hibit 2. exhibit 4 presents most of the data of the implied values for a four-year, option-free, annual-pay bond with a 2.5% coupon based on the information in exhibit 3.exhibit 2 Yield to Maturity Par rates for one-, two-, and Three-Year annual-Pay option-Free bonds
One-Year Two-Year Three-Year 1.25\% 1.50\% 1.70\% exhibit 3 binomial interest rate tree Fit to the Yield Curve (Volatility = 10%)
 exhibit 4 implied Values (in euros) for a 2.5%, Four-Year, option-Free, annual-Pay bond based on exhibit 3
exhibit 4 implied Values (in euros) for a 2.5%, Four-Year, option-Free, annual-Pay bond based on exhibit 3
 black asks about the missing data in exhibits 3 and 4 and directs Sun to complete the following tasks related to those exhibits:
task 1 test that the binomial interest tree has been properly calibrated to be arbitrage-free.
task 2 Develop a spreadsheet model to calculate pathwise valuations. to test the ac-curacy of the spreadsheet, use the data in exhibit 3 and calculate the value of the bond if it takes a path of lowest rates in Year 1 and Year 2 and the second lowest rate in Year 3.
task 3 identify a type of bond where the Monte Carlo calibration method should be used in place of the binomial interest rate method.
task 4 update exhibit 3 to reflect the current volatility, which is now 15%.
-if the assumed volatility is changed as black requested in task 4, the forward rates shown in exhibit 3 will most likely:
black asks about the missing data in exhibits 3 and 4 and directs Sun to complete the following tasks related to those exhibits:
task 1 test that the binomial interest tree has been properly calibrated to be arbitrage-free.
task 2 Develop a spreadsheet model to calculate pathwise valuations. to test the ac-curacy of the spreadsheet, use the data in exhibit 3 and calculate the value of the bond if it takes a path of lowest rates in Year 1 and Year 2 and the second lowest rate in Year 3.
task 3 identify a type of bond where the Monte Carlo calibration method should be used in place of the binomial interest rate method.
task 4 update exhibit 3 to reflect the current volatility, which is now 15%.
-if the assumed volatility is changed as black requested in task 4, the forward rates shown in exhibit 3 will most likely:
(Multiple Choice)
4.8/5  (28)
(28)
The following information relates to Questions
Meredith alvarez is a junior fixed-income analyst with Canzim asset Management. her su-pervisor, Stephanie hartson, asks alvarez to review the asset price and payoff data shown in exhibit 1 to determine whether an arbitrage opportunity exists.exhibit 1 Price and Payoffs for two risk-Free assets
Asset Price Today Payoff in One Year Asset A \ 500 \ 525 Asset B \ 1,000 \ 1,100
hartson also shows alvarez data for a bond that trades in three different markets in the same currency. These data appear in exhibit 2.
exhibit 2 2% Coupon, Five-Year Maturity, annual-Pay bond
New York Hong Kong Mumbai Yield to Maturity 1.9\% 2.3\% 2.0\%
hartson asks alvarez to value two bonds (bond C and bond D) using the binomial tree in exhibit 3. exhibit 4 presents selected data for both bonds.
exhibit 3 binomial interest rate tree with Volatility = 25%
Time 0 Time 1 Time 2 2.7183\% 2.8853\% 1.500\% 1.6487\% 1.7500\% 1.0000\%
exhibit 4 Selected Data on annual-Pay bonds
Bond Maturity Coupon Rate Bond C 2 years 2.5\% Bond D 3 years 3.0\%
hartson tells alvarez that she and her peers have been debating various viewpoints regard-ing the conditions underlying binomial interest rate trees. The following statements were made in the course of the debate.
Statement 1: The only requirements needed to create a binomial interest rate tree are current benchmark interest rates and an assumption about interest rate volatility.
Statement 2: Potential interest rate volatility in a binomial interest rate tree can be es-timated using historical interest rate volatility or observed arket prices from interest rate derivatives.
Statement 3: a bond value derived from a binomial interest rate tree with a relatively
high volatility assumption will be different from the value calculated by discounting the bond's cash flows using current spot rates. based on data in exhibit 5, hartson asks alvarez to calibrate a binomial interest rate tree starting with the calculation of implied forward rates shown in exhibit 6.
exhibit 5 Selected Data for a binomial interest rate tree
Maturity Par Rate Spot Rate 1 2.5000\% 2.5000\% 2 3.5000\% 3.5177\%
exhibit 6 Calibration of binomial interest rate
Tree with Volatility =25\% Time 0 Time 1 5.8365\% 2.500\% Lower one-period forward rate
hartson mentions pathwise valuations as another method to value bonds using a binomial
interest rate tree. using the binomial interest rate tree in exhibit 3, alvarez calculates the pos-sible interest rate paths for bond D shown in exhibit 7.
exhibit 7 interest rate Paths for bond D
Path Time 0 Time 1 Time 2 1 1.500\% 2.8853\% 2.7183\% 2 1.500 2.8853 1.6487 3 1.500 1.7500 1.6487 4 1.500 1.7500 1.0000
before leaving for the day, hartson asks alvarez about the value of using the Monte Carlo method to simulate a large number of potential interest rate paths to value a bond. alvarez makes the following statements.
Statement 4: increasing the number of paths increases the estimate's statistical accuracy.
Statement 5: The bond value derived from aMonte Carlo simulation will be closer to the bond's true fundamental value.
-based on exhibits 5 and 6, the value of the lower one-period forward rate is closest to:
(Multiple Choice)
4.9/5  (39)
(39)
The following information relates to Questions
Meredith alvarez is a junior fixed-income analyst with Canzim asset Management. her su-pervisor, Stephanie hartson, asks alvarez to review the asset price and payoff data shown in exhibit 1 to determine whether an arbitrage opportunity exists.exhibit 1 Price and Payoffs for two risk-Free assets
Asset Price Today Payoff in One Year Asset A \ 500 \ 525 Asset B \ 1,000 \ 1,100
hartson also shows alvarez data for a bond that trades in three different markets in the same currency. These data appear in exhibit 2.
exhibit 2 2% Coupon, Five-Year Maturity, annual-Pay bond
New York Hong Kong Mumbai Yield to Maturity 1.9\% 2.3\% 2.0\%
hartson asks alvarez to value two bonds (bond C and bond D) using the binomial tree in exhibit 3. exhibit 4 presents selected data for both bonds.
exhibit 3 binomial interest rate tree with Volatility = 25%
Time 0 Time 1 Time 2 2.7183\% 2.8853\% 1.500\% 1.6487\% 1.7500\% 1.0000\%
exhibit 4 Selected Data on annual-Pay bonds
Bond Maturity Coupon Rate Bond C 2 years 2.5\% Bond D 3 years 3.0\%
hartson tells alvarez that she and her peers have been debating various viewpoints regard-ing the conditions underlying binomial interest rate trees. The following statements were made in the course of the debate.
Statement 1: The only requirements needed to create a binomial interest rate tree are current benchmark interest rates and an assumption about interest rate volatility.
Statement 2: Potential interest rate volatility in a binomial interest rate tree can be es-timated using historical interest rate volatility or observed arket prices from interest rate derivatives.
Statement 3: a bond value derived from a binomial interest rate tree with a relatively
high volatility assumption will be different from the value calculated by discounting the bond's cash flows using current spot rates. based on data in exhibit 5, hartson asks alvarez to calibrate a binomial interest rate tree starting with the calculation of implied forward rates shown in exhibit 6.
exhibit 5 Selected Data for a binomial interest rate tree
Maturity Par Rate Spot Rate 1 2.5000\% 2.5000\% 2 3.5000\% 3.5177\%
exhibit 6 Calibration of binomial interest rate
Tree with Volatility =25\% Time 0 Time 1 5.8365\% 2.500\% Lower one-period forward rate
hartson mentions pathwise valuations as another method to value bonds using a binomial
interest rate tree. using the binomial interest rate tree in exhibit 3, alvarez calculates the pos-sible interest rate paths for bond D shown in exhibit 7.
exhibit 7 interest rate Paths for bond D
Path Time 0 Time 1 Time 2 1 1.500\% 2.8853\% 2.7183\% 2 1.500 2.8853 1.6487 3 1.500 1.7500 1.6487 4 1.500 1.7500 1.0000
before leaving for the day, hartson asks alvarez about the value of using the Monte Carlo method to simulate a large number of potential interest rate paths to value a bond. alvarez makes the following statements.
Statement 4: increasing the number of paths increases the estimate's statistical accuracy.
Statement 5: The bond value derived from aMonte Carlo simulation will be closer to the bond's true fundamental value.
-based on exhibits 3 and 4, the value of bond C at the upper node at time 1 is closest to:
(Multiple Choice)
4.8/5  (27)
(27)
The following information relates to Questions
Meredith alvarez is a junior fixed-income analyst with Canzim asset Management. her su-pervisor, Stephanie hartson, asks alvarez to review the asset price and payoff data shown in exhibit 1 to determine whether an arbitrage opportunity exists.exhibit 1 Price and Payoffs for two risk-Free assets
Asset Price Today Payoff in One Year Asset A \ 500 \ 525 Asset B \ 1,000 \ 1,100
hartson also shows alvarez data for a bond that trades in three different markets in the same currency. These data appear in exhibit 2.
exhibit 2 2% Coupon, Five-Year Maturity, annual-Pay bond
New York Hong Kong Mumbai Yield to Maturity 1.9\% 2.3\% 2.0\%
hartson asks alvarez to value two bonds (bond C and bond D) using the binomial tree in exhibit 3. exhibit 4 presents selected data for both bonds.
exhibit 3 binomial interest rate tree with Volatility = 25%
Time 0 Time 1 Time 2 2.7183\% 2.8853\% 1.500\% 1.6487\% 1.7500\% 1.0000\%
exhibit 4 Selected Data on annual-Pay bonds
Bond Maturity Coupon Rate Bond C 2 years 2.5\% Bond D 3 years 3.0\%
hartson tells alvarez that she and her peers have been debating various viewpoints regard-ing the conditions underlying binomial interest rate trees. The following statements were made in the course of the debate.
Statement 1: The only requirements needed to create a binomial interest rate tree are current benchmark interest rates and an assumption about interest rate volatility.
Statement 2: Potential interest rate volatility in a binomial interest rate tree can be es-timated using historical interest rate volatility or observed arket prices from interest rate derivatives.
Statement 3: a bond value derived from a binomial interest rate tree with a relatively
high volatility assumption will be different from the value calculated by discounting the bond's cash flows using current spot rates. based on data in exhibit 5, hartson asks alvarez to calibrate a binomial interest rate tree starting with the calculation of implied forward rates shown in exhibit 6.
exhibit 5 Selected Data for a binomial interest rate tree
Maturity Par Rate Spot Rate 1 2.5000\% 2.5000\% 2 3.5000\% 3.5177\%
exhibit 6 Calibration of binomial interest rate
Tree with Volatility =25\% Time 0 Time 1 5.8365\% 2.500\% Lower one-period forward rate
hartson mentions pathwise valuations as another method to value bonds using a binomial
interest rate tree. using the binomial interest rate tree in exhibit 3, alvarez calculates the pos-sible interest rate paths for bond D shown in exhibit 7.
exhibit 7 interest rate Paths for bond D
Path Time 0 Time 1 Time 2 1 1.500\% 2.8853\% 2.7183\% 2 1.500 2.8853 1.6487 3 1.500 1.7500 1.6487 4 1.500 1.7500 1.0000
before leaving for the day, hartson asks alvarez about the value of using the Monte Carlo method to simulate a large number of potential interest rate paths to value a bond. alvarez makes the following statements.
Statement 4: increasing the number of paths increases the estimate's statistical accuracy.
Statement 5: The bond value derived from aMonte Carlo simulation will be closer to the bond's true fundamental value.
-which of the various statements regarding binomial interest rate trees is correct?
(Multiple Choice)
4.8/5  (37)
(37)
The following information relates to Questions
Meredith alvarez is a junior fixed-income analyst with Canzim asset Management. her su-pervisor, Stephanie hartson, asks alvarez to review the asset price and payoff data shown in exhibit 1 to determine whether an arbitrage opportunity exists.exhibit 1 Price and Payoffs for two risk-Free assets
Asset Price Today Payoff in One Year Asset A \ 500 \ 525 Asset B \ 1,000 \ 1,100
hartson also shows alvarez data for a bond that trades in three different markets in the same currency. These data appear in exhibit 2.
exhibit 2 2% Coupon, Five-Year Maturity, annual-Pay bond
New York Hong Kong Mumbai Yield to Maturity 1.9\% 2.3\% 2.0\%
hartson asks alvarez to value two bonds (bond C and bond D) using the binomial tree in exhibit 3. exhibit 4 presents selected data for both bonds.
exhibit 3 binomial interest rate tree with Volatility = 25%
Time 0 Time 1 Time 2 2.7183\% 2.8853\% 1.500\% 1.6487\% 1.7500\% 1.0000\%
exhibit 4 Selected Data on annual-Pay bonds
Bond Maturity Coupon Rate Bond C 2 years 2.5\% Bond D 3 years 3.0\%
hartson tells alvarez that she and her peers have been debating various viewpoints regard-ing the conditions underlying binomial interest rate trees. The following statements were made in the course of the debate.
Statement 1: The only requirements needed to create a binomial interest rate tree are current benchmark interest rates and an assumption about interest rate volatility.
Statement 2: Potential interest rate volatility in a binomial interest rate tree can be es-timated using historical interest rate volatility or observed arket prices from interest rate derivatives.
Statement 3: a bond value derived from a binomial interest rate tree with a relatively
high volatility assumption will be different from the value calculated by discounting the bond's cash flows using current spot rates. based on data in exhibit 5, hartson asks alvarez to calibrate a binomial interest rate tree starting with the calculation of implied forward rates shown in exhibit 6.
exhibit 5 Selected Data for a binomial interest rate tree
Maturity Par Rate Spot Rate 1 2.5000\% 2.5000\% 2 3.5000\% 3.5177\%
exhibit 6 Calibration of binomial interest rate
Tree with Volatility =25\% Time 0 Time 1 5.8365\% 2.500\% Lower one-period forward rate
hartson mentions pathwise valuations as another method to value bonds using a binomial
interest rate tree. using the binomial interest rate tree in exhibit 3, alvarez calculates the pos-sible interest rate paths for bond D shown in exhibit 7.
exhibit 7 interest rate Paths for bond D
Path Time 0 Time 1 Time 2 1 1.500\% 2.8853\% 2.7183\% 2 1.500 2.8853 1.6487 3 1.500 1.7500 1.6487 4 1.500 1.7500 1.0000
before leaving for the day, hartson asks alvarez about the value of using the Monte Carlo method to simulate a large number of potential interest rate paths to value a bond. alvarez makes the following statements.
Statement 4: increasing the number of paths increases the estimate's statistical accuracy.
Statement 5: The bond value derived from aMonte Carlo simulation will be closer to the bond's true fundamental value.
-based on exhibits 3 and 4, the price for bond D is closest to:
(Multiple Choice)
4.9/5  (34)
(34)
The following information relates to Questions
betty tatton is a fixed income analyst with the hedge fund Sailboat asset Management (SaM).SaM invests in a variety of global fixed-income strategies, including fixed-income arbitrage.tatton is responsible for pricing individual investments and analyzing market data to assess the opportunity for arbitrage. She uses two methods to value bonds:
Method 1: Discount each year's cash flow separately using the appropriate interest rate curve.
Method 2: build and use a binomial interest rate tree.
tatton compiles pricing data for a list of annual pay bonds (exhibit 1). each of the bonds will mature in two years, and tatton considers the bonds as being risk-free; both the one-year and two-year benchmark spot rates are 2%. tatton calculates the arbitrage-free prices and identifies an arbitrage opportunity to recommend to her team.exhibit 1 Market Data for Selected bonds
Asset Coupon Market Price Bond A 1\% 98.0584 Bond B 3\% 100.9641 Bond C 5\% 105.8247
next, tatton uses the benchmark yield curve provided in exhibit 2 to consider arbitrage opportunities of both option-free corporate bonds and corporate bonds with embedded op-tions. The benchmark bonds in exhibit 2 pay coupons annually, and the bonds are priced at par.exhibit 2 benchmark Par Curve
Maturity (years) Yield to Maturity (YTM) 1 3.0\% 2 4.0\% 3 5.0\% tatton then identifies three mispriced three-year annual-pay bonds and compiles data onthe bonds (see exhibit 3).
exhibit 3 Market Data of annual-Pay Corporate bonds Company Coupon Market Price Yield Embedded Option? Hutto-Barkley Inc. 3\% 94.9984 5.6\% No Luna y Estrellas Intl. 0\% 88.8996 4.0\% Yes Peaton Scorpio Motors 0\% 83.9619 6.0\% No
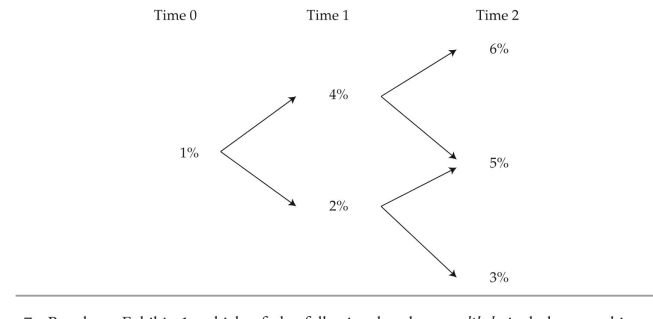
last, tatton identifies two mispriced Swiss bonds, ond x, a three-year bond, and bond Y, a five-year bond. both are annual-pay bonds with a coupon rate of 6%. to calculate the bonds' values, tatton devises the first three years of the interest rate lognormal tree presented in exhibit 4 using historical interest rate volatility data. tatton considers how these data would change if implied volatility, which is higher than historical volatility, were used instead.
exhibit 4 interest rate tree; Forward rates based on Swiss Market
 -Method 1 would most likely not be an appropriate valuation technique for the bond issued by:
-Method 1 would most likely not be an appropriate valuation technique for the bond issued by:
(Multiple Choice)
4.7/5  (35)
(35)
The following information relates to Questions
Meredith alvarez is a junior fixed-income analyst with Canzim asset Management. her su-pervisor, Stephanie hartson, asks alvarez to review the asset price and payoff data shown in exhibit 1 to determine whether an arbitrage opportunity exists.exhibit 1 Price and Payoffs for two risk-Free assets
Asset Price Today Payoff in One Year Asset A \ 500 \ 525 Asset B \ 1,000 \ 1,100
hartson also shows alvarez data for a bond that trades in three different markets in the same currency. These data appear in exhibit 2.
exhibit 2 2% Coupon, Five-Year Maturity, annual-Pay bond
New York Hong Kong Mumbai Yield to Maturity 1.9\% 2.3\% 2.0\%
hartson asks alvarez to value two bonds (bond C and bond D) using the binomial tree in exhibit 3. exhibit 4 presents selected data for both bonds.
exhibit 3 binomial interest rate tree with Volatility = 25%
Time 0 Time 1 Time 2 2.7183\% 2.8853\% 1.500\% 1.6487\% 1.7500\% 1.0000\%
exhibit 4 Selected Data on annual-Pay bonds
Bond Maturity Coupon Rate Bond C 2 years 2.5\% Bond D 3 years 3.0\%
hartson tells alvarez that she and her peers have been debating various viewpoints regard-ing the conditions underlying binomial interest rate trees. The following statements were made in the course of the debate.
Statement 1: The only requirements needed to create a binomial interest rate tree are current benchmark interest rates and an assumption about interest rate volatility.
Statement 2: Potential interest rate volatility in a binomial interest rate tree can be es-timated using historical interest rate volatility or observed arket prices from interest rate derivatives.
Statement 3: a bond value derived from a binomial interest rate tree with a relatively
high volatility assumption will be different from the value calculated by discounting the bond's cash flows using current spot rates. based on data in exhibit 5, hartson asks alvarez to calibrate a binomial interest rate tree starting with the calculation of implied forward rates shown in exhibit 6.
exhibit 5 Selected Data for a binomial interest rate tree
Maturity Par Rate Spot Rate 1 2.5000\% 2.5000\% 2 3.5000\% 3.5177\%
exhibit 6 Calibration of binomial interest rate
Tree with Volatility =25\% Time 0 Time 1 5.8365\% 2.500\% Lower one-period forward rate
hartson mentions pathwise valuations as another method to value bonds using a binomial
interest rate tree. using the binomial interest rate tree in exhibit 3, alvarez calculates the pos-sible interest rate paths for bond D shown in exhibit 7.
exhibit 7 interest rate Paths for bond D
Path Time 0 Time 1 Time 2 1 1.500\% 2.8853\% 2.7183\% 2 1.500 2.8853 1.6487 3 1.500 1.7500 1.6487 4 1.500 1.7500 1.0000
before leaving for the day, hartson asks alvarez about the value of using the Monte Carlo method to simulate a large number of potential interest rate paths to value a bond. alvarez makes the following statements.
Statement 4: increasing the number of paths increases the estimate's statistical accuracy.
Statement 5: The bond value derived from aMonte Carlo simulation will be closer to the bond's true fundamental value.
-based on exhibits 4 and 7, the present value of bond D's cash flows following Path 2 is closest to:
(Multiple Choice)
4.8/5  (35)
(35)
The following information relates to Questions 1-6
katrina black, portfolio manager at Coral bond Management, ltd., is conducting a training session with alex Sun, a junior analyst in the fixed income department. black wants to ex-plain to Sun the arbitrage-free valuation framework used by the firm. black presents Sun with exhibit 1, showing a fictitious bond being traded on three exchanges, and asks Sun to identify the arbitrage opportunity of the bond. Sun agrees to ignore transaction costs in his analysis.exhibit 1 Three-Year, €100 par, 3.00% Coupon, annual-Pay option-Free bond
Eurex NYSE Euronext Frankfurt Price 103.7956 103.7815 103.7565 black shows Sun some exhibits that were part of a recent presentation. exhibit 3 presents most of the data of a binomial lognormal interest rate tree fit to the yield curve shown in ex-hibit 2. exhibit 4 presents most of the data of the implied values for a four-year, option-free, annual-pay bond with a 2.5% coupon based on the information in exhibit 3.exhibit 2 Yield to Maturity Par rates for one-, two-, and Three-Year annual-Pay option-Free bonds
One-Year Two-Year Three-Year 1.25\% 1.50\% 1.70\% exhibit 3 binomial interest rate tree Fit to the Yield Curve (Volatility = 10%)
 exhibit 4 implied Values (in euros) for a 2.5%, Four-Year, option-Free, annual-Pay bond based on exhibit 3
exhibit 4 implied Values (in euros) for a 2.5%, Four-Year, option-Free, annual-Pay bond based on exhibit 3
 black asks about the missing data in exhibits 3 and 4 and directs Sun to complete the following tasks related to those exhibits:
task 1 test that the binomial interest tree has been properly calibrated to be arbitrage-free.
task 2 Develop a spreadsheet model to calculate pathwise valuations. to test the ac-curacy of the spreadsheet, use the data in exhibit 3 and calculate the value of the bond if it takes a path of lowest rates in Year 1 and Year 2 and the second lowest rate in Year 3.
task 3 identify a type of bond where the Monte Carlo calibration method should be used in place of the binomial interest rate method.
task 4 update exhibit 3 to reflect the current volatility, which is now 15%.
-a benefit of performing task 1 is that it:
black asks about the missing data in exhibits 3 and 4 and directs Sun to complete the following tasks related to those exhibits:
task 1 test that the binomial interest tree has been properly calibrated to be arbitrage-free.
task 2 Develop a spreadsheet model to calculate pathwise valuations. to test the ac-curacy of the spreadsheet, use the data in exhibit 3 and calculate the value of the bond if it takes a path of lowest rates in Year 1 and Year 2 and the second lowest rate in Year 3.
task 3 identify a type of bond where the Monte Carlo calibration method should be used in place of the binomial interest rate method.
task 4 update exhibit 3 to reflect the current volatility, which is now 15%.
-a benefit of performing task 1 is that it:
(Multiple Choice)
4.8/5  (33)
(33)
The following information relates to Questions
Meredith alvarez is a junior fixed-income analyst with Canzim asset Management. her su-pervisor, Stephanie hartson, asks alvarez to review the asset price and payoff data shown in exhibit 1 to determine whether an arbitrage opportunity exists.exhibit 1 Price and Payoffs for two risk-Free assets
Asset Price Today Payoff in One Year Asset A \ 500 \ 525 Asset B \ 1,000 \ 1,100
hartson also shows alvarez data for a bond that trades in three different markets in the same currency. These data appear in exhibit 2.
exhibit 2 2% Coupon, Five-Year Maturity, annual-Pay bond
New York Hong Kong Mumbai Yield to Maturity 1.9\% 2.3\% 2.0\%
hartson asks alvarez to value two bonds (bond C and bond D) using the binomial tree in exhibit 3. exhibit 4 presents selected data for both bonds.
exhibit 3 binomial interest rate tree with Volatility = 25%
Time 0 Time 1 Time 2 2.7183\% 2.8853\% 1.500\% 1.6487\% 1.7500\% 1.0000\%
exhibit 4 Selected Data on annual-Pay bonds
Bond Maturity Coupon Rate Bond C 2 years 2.5\% Bond D 3 years 3.0\%
hartson tells alvarez that she and her peers have been debating various viewpoints regard-ing the conditions underlying binomial interest rate trees. The following statements were made in the course of the debate.
Statement 1: The only requirements needed to create a binomial interest rate tree are current benchmark interest rates and an assumption about interest rate volatility.
Statement 2: Potential interest rate volatility in a binomial interest rate tree can be es-timated using historical interest rate volatility or observed arket prices from interest rate derivatives.
Statement 3: a bond value derived from a binomial interest rate tree with a relatively
high volatility assumption will be different from the value calculated by discounting the bond's cash flows using current spot rates. based on data in exhibit 5, hartson asks alvarez to calibrate a binomial interest rate tree starting with the calculation of implied forward rates shown in exhibit 6.
exhibit 5 Selected Data for a binomial interest rate tree
Maturity Par Rate Spot Rate 1 2.5000\% 2.5000\% 2 3.5000\% 3.5177\%
exhibit 6 Calibration of binomial interest rate
Tree with Volatility =25\% Time 0 Time 1 5.8365\% 2.500\% Lower one-period forward rate
hartson mentions pathwise valuations as another method to value bonds using a binomial
interest rate tree. using the binomial interest rate tree in exhibit 3, alvarez calculates the pos-sible interest rate paths for bond D shown in exhibit 7.
exhibit 7 interest rate Paths for bond D
Path Time 0 Time 1 Time 2 1 1.500\% 2.8853\% 2.7183\% 2 1.500 2.8853 1.6487 3 1.500 1.7500 1.6487 4 1.500 1.7500 1.0000
before leaving for the day, hartson asks alvarez about the value of using the Monte Carlo method to simulate a large number of potential interest rate paths to value a bond. alvarez makes the following statements.
Statement 4: increasing the number of paths increases the estimate's statistical accuracy.
Statement 5: The bond value derived from aMonte Carlo simulation will be closer to the bond's true fundamental value.
-based on exhibit 1, alvarez finds that an arbitrage opportunity is:
(Multiple Choice)
4.8/5  (38)
(38)
The following information relates to Questions
betty tatton is a fixed income analyst with the hedge fund Sailboat asset Management (SaM).SaM invests in a variety of global fixed-income strategies, including fixed-income arbitrage.tatton is responsible for pricing individual investments and analyzing market data to assess the opportunity for arbitrage. She uses two methods to value bonds:
Method 1: Discount each year's cash flow separately using the appropriate interest rate curve.
Method 2: build and use a binomial interest rate tree.
tatton compiles pricing data for a list of annual pay bonds (exhibit 1). each of the bonds will mature in two years, and tatton considers the bonds as being risk-free; both the one-year and two-year benchmark spot rates are 2%. tatton calculates the arbitrage-free prices and identifies an arbitrage opportunity to recommend to her team.exhibit 1 Market Data for Selected bonds
Asset Coupon Market Price Bond A 1\% 98.0584 Bond B 3\% 100.9641 Bond C 5\% 105.8247
next, tatton uses the benchmark yield curve provided in exhibit 2 to consider arbitrage opportunities of both option-free corporate bonds and corporate bonds with embedded op-tions. The benchmark bonds in exhibit 2 pay coupons annually, and the bonds are priced at par.exhibit 2 benchmark Par Curve
Maturity (years) Yield to Maturity (YTM) 1 3.0\% 2 4.0\% 3 5.0\% tatton then identifies three mispriced three-year annual-pay bonds and compiles data onthe bonds (see exhibit 3).
exhibit 3 Market Data of annual-Pay Corporate bonds Company Coupon Market Price Yield Embedded Option? Hutto-Barkley Inc. 3\% 94.9984 5.6\% No Luna y Estrellas Intl. 0\% 88.8996 4.0\% Yes Peaton Scorpio Motors 0\% 83.9619 6.0\% No
last, tatton identifies two mispriced Swiss bonds, ond x, a three-year bond, and bond Y, a five-year bond. both are annual-pay bonds with a coupon rate of 6%. to calculate the bonds' values, tatton devises the first three years of the interest rate lognormal tree presented in exhibit 4 using historical interest rate volatility data. tatton considers how these data would change if implied volatility, which is higher than historical volatility, were used instead.
exhibit 4 interest rate tree; Forward rates based on Swiss Market
 -based on exhibit 4 and using Method 2, the correct price for bond x is closest to:
-based on exhibit 4 and using Method 2, the correct price for bond x is closest to:
(Multiple Choice)
4.8/5  (36)
(36)
The following information relates to Questions 1-6
katrina black, portfolio manager at Coral bond Management, ltd., is conducting a training session with alex Sun, a junior analyst in the fixed income department. black wants to ex-plain to Sun the arbitrage-free valuation framework used by the firm. black presents Sun with exhibit 1, showing a fictitious bond being traded on three exchanges, and asks Sun to identify the arbitrage opportunity of the bond. Sun agrees to ignore transaction costs in his analysis.exhibit 1 Three-Year, €100 par, 3.00% Coupon, annual-Pay option-Free bond
Eurex NYSE Euronext Frankfurt Price 103.7956 103.7815 103.7565 black shows Sun some exhibits that were part of a recent presentation. exhibit 3 presents most of the data of a binomial lognormal interest rate tree fit to the yield curve shown in ex-hibit 2. exhibit 4 presents most of the data of the implied values for a four-year, option-free, annual-pay bond with a 2.5% coupon based on the information in exhibit 3.exhibit 2 Yield to Maturity Par rates for one-, two-, and Three-Year annual-Pay option-Free bonds
One-Year Two-Year Three-Year 1.25\% 1.50\% 1.70\% exhibit 3 binomial interest rate tree Fit to the Yield Curve (Volatility = 10%)
 exhibit 4 implied Values (in euros) for a 2.5%, Four-Year, option-Free, annual-Pay bond based on exhibit 3
exhibit 4 implied Values (in euros) for a 2.5%, Four-Year, option-Free, annual-Pay bond based on exhibit 3
 black asks about the missing data in exhibits 3 and 4 and directs Sun to complete the following tasks related to those exhibits:
task 1 test that the binomial interest tree has been properly calibrated to be arbitrage-free.
task 2 Develop a spreadsheet model to calculate pathwise valuations. to test the ac-curacy of the spreadsheet, use the data in exhibit 3 and calculate the value of the bond if it takes a path of lowest rates in Year 1 and Year 2 and the second lowest rate in Year 3.
task 3 identify a type of bond where the Monte Carlo calibration method should be used in place of the binomial interest rate method.
task 4 update exhibit 3 to reflect the current volatility, which is now 15%.
-based on exhibit 1, the best action that an investor should take to profit from the arbitrage opportunity is to:
black asks about the missing data in exhibits 3 and 4 and directs Sun to complete the following tasks related to those exhibits:
task 1 test that the binomial interest tree has been properly calibrated to be arbitrage-free.
task 2 Develop a spreadsheet model to calculate pathwise valuations. to test the ac-curacy of the spreadsheet, use the data in exhibit 3 and calculate the value of the bond if it takes a path of lowest rates in Year 1 and Year 2 and the second lowest rate in Year 3.
task 3 identify a type of bond where the Monte Carlo calibration method should be used in place of the binomial interest rate method.
task 4 update exhibit 3 to reflect the current volatility, which is now 15%.
-based on exhibit 1, the best action that an investor should take to profit from the arbitrage opportunity is to:
(Multiple Choice)
4.8/5  (37)
(37)
The following information relates to Questions 1-6
katrina black, portfolio manager at Coral bond Management, ltd., is conducting a training session with alex Sun, a junior analyst in the fixed income department. black wants to ex-plain to Sun the arbitrage-free valuation framework used by the firm. black presents Sun with exhibit 1, showing a fictitious bond being traded on three exchanges, and asks Sun to identify the arbitrage opportunity of the bond. Sun agrees to ignore transaction costs in his analysis.exhibit 1 Three-Year, €100 par, 3.00% Coupon, annual-Pay option-Free bond
Eurex NYSE Euronext Frankfurt Price 103.7956 103.7815 103.7565 black shows Sun some exhibits that were part of a recent presentation. exhibit 3 presents most of the data of a binomial lognormal interest rate tree fit to the yield curve shown in ex-hibit 2. exhibit 4 presents most of the data of the implied values for a four-year, option-free, annual-pay bond with a 2.5% coupon based on the information in exhibit 3.exhibit 2 Yield to Maturity Par rates for one-, two-, and Three-Year annual-Pay option-Free bonds
One-Year Two-Year Three-Year 1.25\% 1.50\% 1.70\% exhibit 3 binomial interest rate tree Fit to the Yield Curve (Volatility = 10%)
 exhibit 4 implied Values (in euros) for a 2.5%, Four-Year, option-Free, annual-Pay bond based on exhibit 3
exhibit 4 implied Values (in euros) for a 2.5%, Four-Year, option-Free, annual-Pay bond based on exhibit 3
 black asks about the missing data in exhibits 3 and 4 and directs Sun to complete the following tasks related to those exhibits:
task 1 test that the binomial interest tree has been properly calibrated to be arbitrage-free.
task 2 Develop a spreadsheet model to calculate pathwise valuations. to test the ac-curacy of the spreadsheet, use the data in exhibit 3 and calculate the value of the bond if it takes a path of lowest rates in Year 1 and Year 2 and the second lowest rate in Year 3.
task 3 identify a type of bond where the Monte Carlo calibration method should be used in place of the binomial interest rate method.
task 4 update exhibit 3 to reflect the current volatility, which is now 15%.
-which of the following statements about the missing data in exhibit 3 is correct?
black asks about the missing data in exhibits 3 and 4 and directs Sun to complete the following tasks related to those exhibits:
task 1 test that the binomial interest tree has been properly calibrated to be arbitrage-free.
task 2 Develop a spreadsheet model to calculate pathwise valuations. to test the ac-curacy of the spreadsheet, use the data in exhibit 3 and calculate the value of the bond if it takes a path of lowest rates in Year 1 and Year 2 and the second lowest rate in Year 3.
task 3 identify a type of bond where the Monte Carlo calibration method should be used in place of the binomial interest rate method.
task 4 update exhibit 3 to reflect the current volatility, which is now 15%.
-which of the following statements about the missing data in exhibit 3 is correct?
(Multiple Choice)
4.9/5  (37)
(37)
The following information relates to Questions
betty tatton is a fixed income analyst with the hedge fund Sailboat asset Management (SaM).SaM invests in a variety of global fixed-income strategies, including fixed-income arbitrage.tatton is responsible for pricing individual investments and analyzing market data to assess the opportunity for arbitrage. She uses two methods to value bonds:
Method 1: Discount each year's cash flow separately using the appropriate interest rate curve.
Method 2: build and use a binomial interest rate tree.
tatton compiles pricing data for a list of annual pay bonds (exhibit 1). each of the bonds will mature in two years, and tatton considers the bonds as being risk-free; both the one-year and two-year benchmark spot rates are 2%. tatton calculates the arbitrage-free prices and identifies an arbitrage opportunity to recommend to her team.exhibit 1 Market Data for Selected bonds
Asset Coupon Market Price Bond A 1\% 98.0584 Bond B 3\% 100.9641 Bond C 5\% 105.8247
next, tatton uses the benchmark yield curve provided in exhibit 2 to consider arbitrage opportunities of both option-free corporate bonds and corporate bonds with embedded op-tions. The benchmark bonds in exhibit 2 pay coupons annually, and the bonds are priced at par.exhibit 2 benchmark Par Curve
Maturity (years) Yield to Maturity (YTM) 1 3.0\% 2 4.0\% 3 5.0\% tatton then identifies three mispriced three-year annual-pay bonds and compiles data onthe bonds (see exhibit 3).
exhibit 3 Market Data of annual-Pay Corporate bonds Company Coupon Market Price Yield Embedded Option? Hutto-Barkley Inc. 3\% 94.9984 5.6\% No Luna y Estrellas Intl. 0\% 88.8996 4.0\% Yes Peaton Scorpio Motors 0\% 83.9619 6.0\% No
last, tatton identifies two mispriced Swiss bonds, ond x, a three-year bond, and bond Y, a five-year bond. both are annual-pay bonds with a coupon rate of 6%. to calculate the bonds' values, tatton devises the first three years of the interest rate lognormal tree presented in exhibit 4 using historical interest rate volatility data. tatton considers how these data would change if implied volatility, which is higher than historical volatility, were used instead.
exhibit 4 interest rate tree; Forward rates based on Swiss Market
 -based on exhibit 1, which of the following bonds most likely includes an arbitrage opportunity?
-based on exhibit 1, which of the following bonds most likely includes an arbitrage opportunity?
(Multiple Choice)
4.9/5  (32)
(32)
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)