Exam 10: Parametric Equations and Polar Coordinates
Exam 1: Functions and Models179 Questions
Exam 2: Limits and Derivatives139 Questions
Exam 3: Differentiation Rules160 Questions
Exam 4: Applications of Differentiation160 Questions
Exam 5: Integrals158 Questions
Exam 6: Applications of Integration157 Questions
Exam 7: Techniques of Integration160 Questions
Exam 8: Further Applications of Integration160 Questions
Exam 9: Differential Equations160 Questions
Exam 10: Parametric Equations and Polar Coordinates160 Questions
Exam 11: Infinite Sequences and Series159 Questions
Exam 12: Vectors and the Geometry of Space160 Questions
Exam 13: Vector Functions159 Questions
Exam 14: Partial Derivatives158 Questions
Exam 15: Multiple Integrals159 Questions
Exam 16: Vector Calculus159 Questions
Exam 17: Second-Order Differential Equations159 Questions
Select questions type
Find an equation of the hyperbola centered at the origin that satisfies the given condition.
Vertices: , asymptotes:
(Short Answer)
4.8/5  (33)
(33)
Find the point(s) on the curve where the tangent is horizontal.
(Multiple Choice)
4.8/5  (43)
(43)
The planet Mercury travels in an elliptical orbit with eccentricity 0.703. Its minimum distance from the Sun is . If the perihelion distance from a planet to the Sun is and the aphelion distance is , find the maximum distance (in ) from Mercury to the Sun.
Select the correct answer.
(Multiple Choice)
4.9/5  (34)
(34)
Write a polar equation in and of an ellipse with the focus at the origin, with the eccentricity and directrix .
(Short Answer)
4.8/5  (39)
(39)
Find parametric equations to represent the line segment from to . Select the correct answer.
(Multiple Choice)
4.9/5  (42)
(42)
If a projectile is fired with an initial velocity of meters per second at an angle above the horizontal and air resistance is assumed to be negligible, then its position after seconds is given by the parametric equations
where is the acceleration of gravity . If a gun is fired with and when will the bullet hit the ground?
(Multiple Choice)
4.7/5  (38)
(38)
Graph of the following curve is given. Find its length. Select the correct answer.
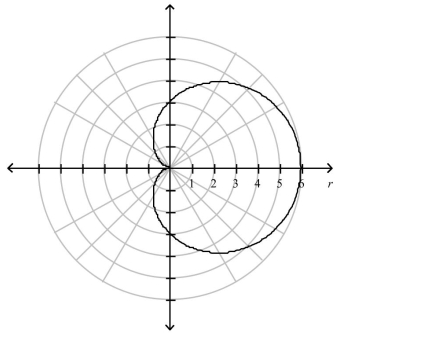
(Multiple Choice)
4.8/5  (34)
(34)
Write a polar equation in and of an ellipse with the focus at the origin, with the eccentricity and directrix .
(Multiple Choice)
4.8/5  (39)
(39)
Find parametric equations to represent the line segment from to .
(Multiple Choice)
4.8/5  (28)
(28)
The planet Mercury travels in an elliptical orbit with eccentricity . Its minimum distance from the Sun is . If the perihelion distance from a planet to the Sun is and the aphelion distance is , find the maximum distance (in km) from Mercury to the Sun.
(Multiple Choice)
4.8/5  (43)
(43)
Write a polar equation in and of an ellipse with the focus at the origin, with the eccentricity and directrix .
(Multiple Choice)
4.8/5  (36)
(36)
Find an equation for the conic that satisfies the given conditions. ellipse, foci , length of major axis 8
(Short Answer)
4.8/5  (39)
(39)
Find the point(s) on the curve where the tangent is horizontal. Select the correct answer.
(Multiple Choice)
4.8/5  (36)
(36)
Find the point(s) on the curve where the tangent is horizontal.
(Short Answer)
4.8/5  (32)
(32)
Find parametric equations to represent the line segment from to . Select the correct answer.
(Multiple Choice)
4.9/5  (32)
(32)
Find parametric equations for the path of a particle that moves once clockwise along the circle , starting at .
(Short Answer)
4.8/5  (41)
(41)
Find the surface area generated by rotating the lemniscate about the line .
(Multiple Choice)
4.8/5  (35)
(35)
Find an equation for the conic that satisfies the given conditions. Select the correct answer.
ellipse, foci , length of major axis 8
(Multiple Choice)
5.0/5  (34)
(34)
Showing 141 - 160 of 160
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)