Exam 7: Techniques of Integration
Exam 1: Functions and Models179 Questions
Exam 2: Limits and Derivatives139 Questions
Exam 3: Differentiation Rules160 Questions
Exam 4: Applications of Differentiation160 Questions
Exam 5: Integrals158 Questions
Exam 6: Applications of Integration157 Questions
Exam 7: Techniques of Integration160 Questions
Exam 8: Further Applications of Integration160 Questions
Exam 9: Differential Equations160 Questions
Exam 10: Parametric Equations and Polar Coordinates160 Questions
Exam 11: Infinite Sequences and Series159 Questions
Exam 12: Vectors and the Geometry of Space160 Questions
Exam 13: Vector Functions159 Questions
Exam 14: Partial Derivatives158 Questions
Exam 15: Multiple Integrals159 Questions
Exam 16: Vector Calculus159 Questions
Exam 17: Second-Order Differential Equations159 Questions
Select questions type
Find the average value of the function in the interval .
Free
(Multiple Choice)
4.9/5  (38)
(38)
Correct Answer:
B
Use the Trapezoidal Rule to approximate the integral with answers rounded to four decimal places.
Free
(Short Answer)
4.7/5  (38)
(38)
Correct Answer:
0.2029
Use the Midpoint Rule to approximate the given integral with the specified value of . Compare your result to the actual value. Find the error in the approximation.
Free
(Short Answer)
4.9/5  (27)
(27)
Correct Answer:
0.00008
Evaluate the integral using an appropriate trigonometric substitution.
(Short Answer)
4.9/5  (32)
(32)
Let and be real numbers. What integral must appear in place of the question mark "?" to make the following statement true?
(Multiple Choice)
5.0/5  (30)
(30)
Estimate the area of the shaded region by using the Trapezoidal Rule with . Round the answer to the nearest tenth.
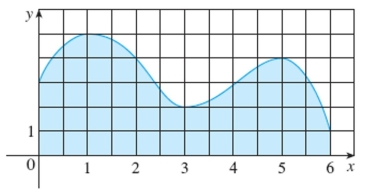
(Short Answer)
4.9/5  (39)
(39)
Find the volume of the resulting solid if the region under the curve
from to is rotated about the -axis. Round your answer to four decimal places.
(Short Answer)
4.8/5  (29)
(29)
The region under the curve is rotated about the -axis. Find the volume of the resulting solid.
(Short Answer)
4.8/5  (32)
(32)
Use Simpson's Rule to approximate the integral with answers rounded to four decimal places.
(Short Answer)
4.7/5  (35)
(35)
Showing 1 - 20 of 160
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)