Exam 10: Parametric Equations and Polar Coordinates
Exam 1: Functions and Models179 Questions
Exam 2: Limits and Derivatives139 Questions
Exam 3: Differentiation Rules160 Questions
Exam 4: Applications of Differentiation160 Questions
Exam 5: Integrals158 Questions
Exam 6: Applications of Integration157 Questions
Exam 7: Techniques of Integration160 Questions
Exam 8: Further Applications of Integration160 Questions
Exam 9: Differential Equations160 Questions
Exam 10: Parametric Equations and Polar Coordinates160 Questions
Exam 11: Infinite Sequences and Series159 Questions
Exam 12: Vectors and the Geometry of Space160 Questions
Exam 13: Vector Functions159 Questions
Exam 14: Partial Derivatives158 Questions
Exam 15: Multiple Integrals159 Questions
Exam 16: Vector Calculus159 Questions
Exam 17: Second-Order Differential Equations159 Questions
Select questions type
Find the vertices, foci and asymptotes of the hyperbola.
Free
(Multiple Choice)
4.9/5  (32)
(32)
Correct Answer:
B, C
Set up an integral that represents the length of the curve. Then use your calculator to find the length correct to four decimal places.
Free
(Short Answer)
4.9/5  (28)
(28)
Correct Answer:
Find the area of the region that is bounded by the given curve and lies in the specified sector.
(Short Answer)
5.0/5  (29)
(29)
In the LORAN (LOng RAnge Navigation) radio navigation system, two radio stations located at and transmit simultaneous signals to a ship or an aircraft located at . The onboard computer converts the time difference in receiving these signals into a distance difference , and this, according to the definition of a hyperbola, locates the ship or aircraft on one branch of a hyperbola (see the figure).
Suppose that station is located due east of station on a coastline. A ship received the signal from microseconds before it received the signal from . Assuming that radio signals travel at a speed of and if the ship is due north of , how far off the coastline is the ship? Round your answer to the nearest mile. Select the correct answer.
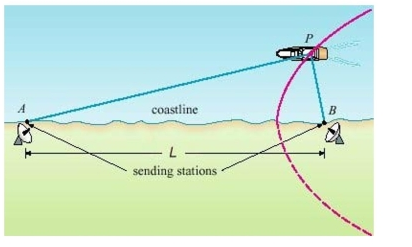
(Multiple Choice)
4.8/5  (27)
(27)
Find the area of the region that lies inside the first curve and outside the second curve.
(Multiple Choice)
4.9/5  (34)
(34)
If the parametric curve satisfies , then it has a horizontal tangent when .
(True/False)
4.8/5  (33)
(33)
Find an equation of the tangent to the curve at the point corresponding to the given value of the parameter.
(Short Answer)
4.8/5  (32)
(32)
Describe the motion of a particle with position as varies in the given interval .
(Short Answer)
4.9/5  (30)
(30)
Find the area of the region that lies inside the first curve and outside the second curve.
(Short Answer)
4.7/5  (26)
(26)
Set up, but do not evaluate, an integral that represents the length of the parametric curve.
(Short Answer)
4.8/5  (32)
(32)
Find an equation of the ellipse that satisfies the given conditions. Foci: , vertices
(Short Answer)
5.0/5  (23)
(23)
Eliminate the parameter to find a Cartesian equation of the curve.
(Short Answer)
4.9/5  (33)
(33)
The orbit of Hale-Bopp comet, discovered in 1995, is an ellipse with eccentricity and one focus at the Sun. The length of its major axis is . [An astronomical unit (AU) is the mean distance between Earth and the Sun, about 93 million miles.] Find the maximum distance from the comet to the Sun. (The perihelion distance from a planet to the Sun is and the aphelion distance is .) Find the answer in AU and round to the nearest hundredth.
(Short Answer)
4.8/5  (37)
(37)
Write a polar equation in and of a hyperbola with the focus at the origin, with the eccentricity 7 and directrix .
(Multiple Choice)
4.9/5  (26)
(26)
Find the exact area of the surface obtained by rotating the given curve about the -axis.
(Multiple Choice)
4.9/5  (33)
(33)
Showing 1 - 20 of 160
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)