Exam 10: Further Applications of the Derivative
Exam 1: Fundamental Concepts of Algebra119 Questions
Exam 2: Equations and Inequalities94 Questions
Exam 3: Functions and Graphs96 Questions
Exam 4: Polynomial and Rational Functions105 Questions
Exam 5: Exponential and Logarithmic Functions94 Questions
Exam 6: Systems of Equations and Inequalities96 Questions
Exam 7: Matrices and Determinants94 Questions
Exam 8: Limits and Derivatives77 Questions
Exam 9: Applications of the Derivative83 Questions
Exam 10: Further Applications of the Derivative83 Questions
Exam 11: Derivatives of Exponential and Logarithmic Functions121 Questions
Exam 12: Integration and Its Applications74 Questions
Exam 13: Techniques of Integration50 Questions
Exam 14: Functions of Several Variables92 Questions
Exam 15: Trigonometric Functions Web60 Questions
Exam 16: Series and Taylor Polynomials Web127 Questions
Exam 17: Probability Web89 Questions
Select questions type
This problem contains a function and its graph, where Use the graph to determine, as well as you can, the horizontal asymptote. Check your conclusion by using the function to determine the horizontal asymptote analytically. 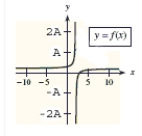
(Multiple Choice)
4.7/5  (41)
(41)
Use analytic methods to find the limit as for the given function.
(Multiple Choice)
4.8/5  (37)
(37)
A firm has total revenue given by for x units of a product. Find the maximum revenue from sales of that product.
(Multiple Choice)
4.9/5  (33)
(33)
Complete the table for the function . Let x = 4. dx=\Deltaxdy\Deltay\Deltay-dydy/\Deltay 1.00000 0.50000 0.10000
(Multiple Choice)
4.7/5  (35)
(35)
The revenue R for a company selling x units is . Use differentials to approximate the change in revenue if sales increase from to units.
(Multiple Choice)
4.9/5  (44)
(44)
A business has a cost (in dollars) of for producing x units. What is the limit of as x approaches infinity?
(Multiple Choice)
4.8/5  (30)
(30)
Complete the table for the function . Let x = 4. dx=\Deltax dy \Deltay \Deltay-dy dy/\Deltay 5.00000 2.50000 0.50000
(Multiple Choice)
4.9/5  (46)
(46)
The measurement of the edge of a cube is found to be 8 inches, with a possible error of 0.08 inch. Use differentials to estimate the propagated error in computing (a) the volume of the cube and (b) the surface area of the cube. Give your answers to two decimal places.
(Multiple Choice)
4.8/5  (34)
(34)
Find the speed v, in miles per hour, that will minimize costs on a 125-mile delivery trip. The cost per hour for fuel is dollars, and the driver is paid dollars per hour. (Assume there are no costs other than wages and fuel.)
(Multiple Choice)
4.7/5  (30)
(30)
Determine the dimensions of a rectangular solid (with a square base) with maximum volume if its surface area is 400 square meters.
(Multiple Choice)
4.8/5  (40)
(40)
Sketch the graph of the relation using any extrema, intercepts, symmetry, and asymptotes.
(Multiple Choice)
4.8/5  (34)
(34)
A Norman window is constructed by adjoining a semicircle to the top of an ordinary rectangular window (see figure). Find the dimensions of a Norman window of maximum area if the total perimeter is 24 feet. Round yours answers to two decimal places. 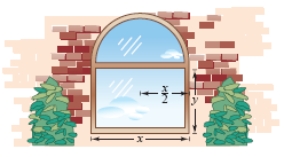
(Multiple Choice)
4.9/5  (32)
(32)
A rancher has 320 feet of fencing to enclose two adjacent rectangular corrals (see figure). What dimensions should be used so that the enclosed area will be a maximum? 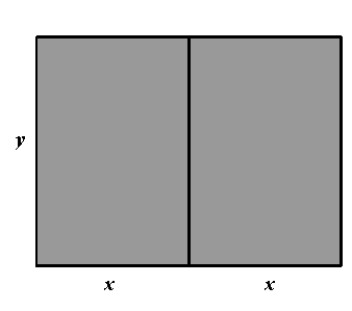
(Multiple Choice)
4.9/5  (37)
(37)
Compare dy and for at x = 1 with dx = 0.03. Give your answers to four decimal places.
(Multiple Choice)
4.8/5  (26)
(26)
A function and its graph are given. Use the graph to find the horizontal asymptotes, if they exist. Confirm your results analytically. 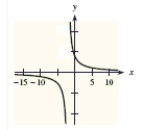
(Multiple Choice)
4.8/5  (36)
(36)
Showing 61 - 80 of 83
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)