Exam 12: Integration and Its Applications
Exam 1: Fundamental Concepts of Algebra119 Questions
Exam 2: Equations and Inequalities94 Questions
Exam 3: Functions and Graphs96 Questions
Exam 4: Polynomial and Rational Functions105 Questions
Exam 5: Exponential and Logarithmic Functions94 Questions
Exam 6: Systems of Equations and Inequalities96 Questions
Exam 7: Matrices and Determinants94 Questions
Exam 8: Limits and Derivatives77 Questions
Exam 9: Applications of the Derivative83 Questions
Exam 10: Further Applications of the Derivative83 Questions
Exam 11: Derivatives of Exponential and Logarithmic Functions121 Questions
Exam 12: Integration and Its Applications74 Questions
Exam 13: Techniques of Integration50 Questions
Exam 14: Functions of Several Variables92 Questions
Exam 15: Trigonometric Functions Web60 Questions
Exam 16: Series and Taylor Polynomials Web127 Questions
Exam 17: Probability Web89 Questions
Select questions type
Use algebra to rewrite the integrand; then integrate and simplify.
Free
(Multiple Choice)
4.9/5  (33)
(33)
Correct Answer:
B
Estimate the surface area of the pond shown in the figure using the Midpoint Rule. 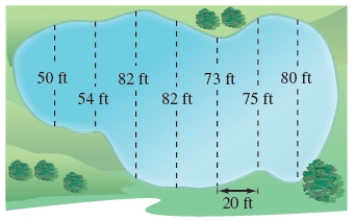
Free
(Multiple Choice)
4.8/5  (28)
(28)
Correct Answer:
B
Find the area of the region bounded by the graphs of the algebraic functions. f(x)=+18x+81 g(x)=11(x+9)
(Multiple Choice)
4.8/5  (29)
(29)
Find the indefinite integral and check the result by differentiation.
(Multiple Choice)
4.9/5  (29)
(29)
Use the Midpoint Rule with to approximate where . Then use a graphing utility to evaluate the definite integral. Compare your results.
(Multiple Choice)
4.8/5  (36)
(36)
Find the equation of the function whose derivative is and whose graph passes through the point .
(Multiple Choice)
4.9/5  (29)
(29)
Evaluate the following definite integral. Use a graphing utility to check your answer.
(Multiple Choice)
4.9/5  (38)
(38)
Find the indefinite integral of the following function and check the result by differentiation.
(Multiple Choice)
4.7/5  (31)
(31)
Use the Midpoint Rule with n = 4 to approximate the area of the region bounded by the graph of and the x-axis over the interval [ ].
(Multiple Choice)
4.8/5  (29)
(29)
The revenue from a manufacturing process (in millions of dollars per year) is projected to follow the model for 10 years. Over the same period of time, the cost (in millions of dollars per year) is projected to follow the model , where t is the time (in years). Approximate the profit over the 10-year period, beginning with t = 0. Round your answer to two decimal places.
(Multiple Choice)
4.9/5  (30)
(30)
Set up the definite integral that gives the area of the region bounded by the graphs. f(x)=(x-4 g(x)=x-4 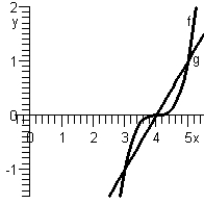
(Multiple Choice)
4.9/5  (32)
(32)
Find the cost function for the marginal cost and fixed cost of (for x = 0).
(Multiple Choice)
4.8/5  (27)
(27)
Showing 1 - 20 of 74
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)