Exam 14: Functions of Several Variables
Exam 1: Fundamental Concepts of Algebra119 Questions
Exam 2: Equations and Inequalities94 Questions
Exam 3: Functions and Graphs96 Questions
Exam 4: Polynomial and Rational Functions105 Questions
Exam 5: Exponential and Logarithmic Functions94 Questions
Exam 6: Systems of Equations and Inequalities96 Questions
Exam 7: Matrices and Determinants94 Questions
Exam 8: Limits and Derivatives77 Questions
Exam 9: Applications of the Derivative83 Questions
Exam 10: Further Applications of the Derivative83 Questions
Exam 11: Derivatives of Exponential and Logarithmic Functions121 Questions
Exam 12: Integration and Its Applications74 Questions
Exam 13: Techniques of Integration50 Questions
Exam 14: Functions of Several Variables92 Questions
Exam 15: Trigonometric Functions Web60 Questions
Exam 16: Series and Taylor Polynomials Web127 Questions
Exam 17: Probability Web89 Questions
Select questions type
Find three positive numbers x, y, and z whose sum is 33 and product is a maximum.
Free
(Multiple Choice)
4.9/5  (29)
(29)
Correct Answer:
B
Sketch the level curves for the function below for the given values .
Free
(Multiple Choice)
4.9/5  (33)
(33)
Correct Answer:
E
Find the the distance between the two points and .
Free
(Multiple Choice)
4.9/5  (35)
(35)
Correct Answer:
C
Use a double integral to find the volume of the solid bounded by the graphs of the equations.
(Multiple Choice)
4.9/5  (29)
(29)
A company manufactures two types of sneakers: running shoes and basketball shoes. The total revenue from x1 units of running shoes and y1 units of basketball shoes is: , where x1 and x2 are in thousands of units. Find x1 and x2 so as to maximize the revenue.
(Multiple Choice)
4.9/5  (41)
(41)
Use a double integral to find the volume of the indicated solid. 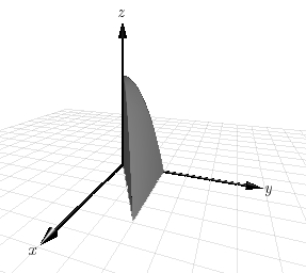
(Multiple Choice)
4.7/5  (32)
(32)
A store manager wants to know the demand y for an energy bar as a function of price x. The daily sales for three different prices of the energy bar are shown in the table. Price, x
$ 1.02
$ 1.23
$ 1.54
Demand, y
410
365
280
(i) Use the regression capabilities of a graphing utility to find the least squares regression line for the data.
(ii) Use the model to estimate the demand when the price is $1.38.
(Multiple Choice)
4.7/5  (35)
(35)
A manufacturer estimates the Cobb-Douglas production function to be given by . Estimate the production levels when and .
(Multiple Choice)
4.8/5  (32)
(32)
Find the least squares regression line for the given points. Then plot the points and sketch the regression line.
(Multiple Choice)
4.7/5  (36)
(36)
Sketch the trace of the intersection of plane y = 4 with the sphere: .
(Multiple Choice)
5.0/5  (36)
(36)
Determine whether there is a relative maximum, a relative minimum, a saddle point, or insufficient information to determine the nature of the function at the critical point . Given: , =-1 , =-8 , =5
(Multiple Choice)
4.7/5  (30)
(30)
Determine whether the statement is true or false. If it is false, explain why or give an example that shows it is false. When the correlation coefficient is , the model is a good fit.
(Multiple Choice)
4.9/5  (24)
(24)
A rancher plans to use an existing stone wall and the side of a barn as a boundary for two adjacent rectangular corrals. Fencing for the perimeter costs 15 per foot. To separate the corrals, a fence that costs 6 per foot will divide the region. The total area of the two corrals is to be square feet. Use Lagrange multipliers to find the dimensions that will minimize the cost of the fencing. 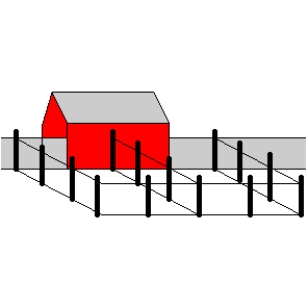
(Multiple Choice)
4.9/5  (31)
(31)
Examine the function given below for relative extrema and saddle points.
(Multiple Choice)
4.8/5  (40)
(40)
Find the average value of over the region R: square with vertices .
(Multiple Choice)
4.8/5  (33)
(33)
Describe the level curves of the function. Sketch the level curves for the given c-values. , c = 0, 2, 4, 6
(Multiple Choice)
4.8/5  (34)
(34)
Showing 1 - 20 of 92
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)