Exam 16: Series and Taylor Polynomials Web
Exam 1: Fundamental Concepts of Algebra119 Questions
Exam 2: Equations and Inequalities94 Questions
Exam 3: Functions and Graphs96 Questions
Exam 4: Polynomial and Rational Functions105 Questions
Exam 5: Exponential and Logarithmic Functions94 Questions
Exam 6: Systems of Equations and Inequalities96 Questions
Exam 7: Matrices and Determinants94 Questions
Exam 8: Limits and Derivatives77 Questions
Exam 9: Applications of the Derivative83 Questions
Exam 10: Further Applications of the Derivative83 Questions
Exam 11: Derivatives of Exponential and Logarithmic Functions121 Questions
Exam 12: Integration and Its Applications74 Questions
Exam 13: Techniques of Integration50 Questions
Exam 14: Functions of Several Variables92 Questions
Exam 15: Trigonometric Functions Web60 Questions
Exam 16: Series and Taylor Polynomials Web127 Questions
Exam 17: Probability Web89 Questions
Select questions type
Write an expression for the nth term of the sequence .
Free
(Multiple Choice)
4.8/5  (32)
(32)
Correct Answer:
A
Find the limit of the following sequence.
Free
(Multiple Choice)
4.9/5  (37)
(37)
Correct Answer:
E
Use the Ratio Test to determine the convergence or divergence of the series .
Free
(Multiple Choice)
4.9/5  (39)
(39)
Correct Answer:
A
Use a symbolic differentiation utility to find the Taylor polynomials (centred at zero) of degrees (a) 2, (b) 4, (c) 6, (d) 8.
(Multiple Choice)
4.8/5  (34)
(34)
Use Newton's Method to approximate the zero(s) of the function accurate to three decimal places.
(Multiple Choice)
4.8/5  (37)
(37)
Determine whether the sequence is arithmetic. If so, find the common difference. (Assume that n begins with 1.)
(Multiple Choice)
4.8/5  (34)
(34)
Find the sum of the finite geometric series. Round to the nearest hundredth.
(Multiple Choice)
4.9/5  (28)
(28)
Use the Ratio Test to determine the convergence or divergence of the series.
(Multiple Choice)
4.8/5  (45)
(45)
Apply Taylor's Theorem to find the power series centered at for the function .
(Multiple Choice)
4.9/5  (42)
(42)
Find the indicated nth term of the geometric sequence. 7th term:
(Multiple Choice)
4.9/5  (28)
(28)
Determine the convergence or divergence of the following series. Use a symbolic algebra utility to verify your result.
(Multiple Choice)
4.7/5  (37)
(37)
The repeating decimal is expressed as a geometric series . Write the decimal as the ratio of two integers.
(Multiple Choice)
4.9/5  (32)
(32)
Write the first five terms of the sequence of partial sums.
(Multiple Choice)
4.7/5  (42)
(42)
Approximate, to three decimal places, the x-value of the point of intersection of the graphs of f(x) and g(x). Round your answer to three decimal places. 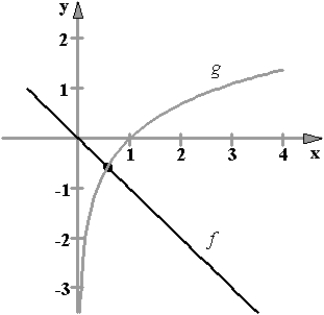
(Multiple Choice)
4.9/5  (40)
(40)
Determine the maximum error guaranteed by Taylor's Theorem with Remainder when the fifth-degree Taylor polynomial is used to approximate in the interval centered at 0. Round your answer to five decimal places.
(Multiple Choice)
4.9/5  (36)
(36)
Showing 1 - 20 of 127
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)