Exam 17: Probability Web
Exam 1: Fundamental Concepts of Algebra119 Questions
Exam 2: Equations and Inequalities94 Questions
Exam 3: Functions and Graphs96 Questions
Exam 4: Polynomial and Rational Functions105 Questions
Exam 5: Exponential and Logarithmic Functions94 Questions
Exam 6: Systems of Equations and Inequalities96 Questions
Exam 7: Matrices and Determinants94 Questions
Exam 8: Limits and Derivatives77 Questions
Exam 9: Applications of the Derivative83 Questions
Exam 10: Further Applications of the Derivative83 Questions
Exam 11: Derivatives of Exponential and Logarithmic Functions121 Questions
Exam 12: Integration and Its Applications74 Questions
Exam 13: Techniques of Integration50 Questions
Exam 14: Functions of Several Variables92 Questions
Exam 15: Trigonometric Functions Web60 Questions
Exam 16: Series and Taylor Polynomials Web127 Questions
Exam 17: Probability Web89 Questions
Select questions type
A sales representative makes a sale at approximately one-third of the businesses he calls on. On a given day, he goes to four businesses. What is the probability that he will make a sale at all four businesses?
Free
(Multiple Choice)
4.9/5  (32)
(32)
Correct Answer:
D
A coin is tossed three times. Describe the event A that at least two heads occur.
Free
(Multiple Choice)
5.0/5  (29)
(29)
Correct Answer:
C
There are 11 patients in Dr. Ziglar's waiting room. Dr. Ziglar can see 5 patients before lunch. In how many different orders can Dr. Ziglar see 5 of the patients before lunch?
(Multiple Choice)
4.8/5  (37)
(37)
In a survey, Americans were asked how well informed they are about new scientific discoveries. The results are shown in the pie graph below. 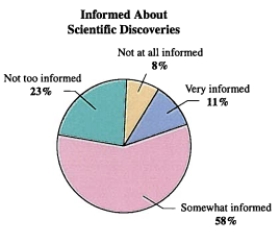 If two people from the survey are chosen at random, what is the probability that neither person feels very informed about scientific discoveries? Round to the nearest ten-thousandth.
If two people from the survey are chosen at random, what is the probability that neither person feels very informed about scientific discoveries? Round to the nearest ten-thousandth.
(Multiple Choice)
4.9/5  (34)
(34)
A meteorologist predicts that the amount of rainfall (in inches) expected for a certain coastal community during a hurricane has the probability density function . Find and interpret the probability .
(Multiple Choice)
4.8/5  (40)
(40)
Expand the binomial by using Pascal's triangle to determine the coefficients. Show your work.
(Essay)
4.8/5  (39)
(39)
Two six-sided dice are tossed. Find the probability that the sum is odd.
(Multiple Choice)
4.9/5  (37)
(37)
Sketch a graph of the probability distribution. x 0 1 2 3 4 P(x)
(Multiple Choice)
4.8/5  (43)
(43)
Seven cards are chosen at random from a standard deck of playing cards. In how many ways can the cards be chosen if all seven cards are spades.
(Multiple Choice)
4.7/5  (35)
(35)
Find the specified nth term in the expansion of the binomial.
(Multiple Choice)
4.8/5  (41)
(41)
A combination lock will open when the right choice of three numbers (from 1 to 32) is selected. How many different lock combinations are possible?
(Multiple Choice)
4.9/5  (35)
(35)
Buses arrive and depart from a college every 25 minutes. The probability density function for the waiting time t (in minutes) for a person arriving at the bus stop is on the interval . Find the probability that the person will wait no longer than 10 minutes.
(Multiple Choice)
4.7/5  (39)
(39)
A biology instructor gives her class a list of eight study problems, from which she will select five to be answered on an exam. A student knows how to solve six of the problems. Find the probability that the student will be able to answer all five questions on the exam.
(Multiple Choice)
4.7/5  (35)
(35)
Find the mean, variance, and standard deviation of the normal density function over . Do not use integration.
(Multiple Choice)
4.8/5  (35)
(35)
A state lottery game requires a person to select ten different numbers from thirty-three numbers. The order of the selection is not important. In how many ways can this be done?
(Multiple Choice)
5.0/5  (40)
(40)
Use mathematical induction to prove the formula for every positive integer n. Show all your work.
(Essay)
5.0/5  (32)
(32)
Determine the number of ways a computer can randomly generate an integer divisible by 4 from 1 through 15.
(Multiple Choice)
4.8/5  (35)
(35)
Showing 1 - 20 of 89
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)