Exam 10: Further Applications of the Derivative
Exam 1: Fundamental Concepts of Algebra119 Questions
Exam 2: Equations and Inequalities94 Questions
Exam 3: Functions and Graphs96 Questions
Exam 4: Polynomial and Rational Functions105 Questions
Exam 5: Exponential and Logarithmic Functions94 Questions
Exam 6: Systems of Equations and Inequalities96 Questions
Exam 7: Matrices and Determinants94 Questions
Exam 8: Limits and Derivatives77 Questions
Exam 9: Applications of the Derivative83 Questions
Exam 10: Further Applications of the Derivative83 Questions
Exam 11: Derivatives of Exponential and Logarithmic Functions121 Questions
Exam 12: Integration and Its Applications74 Questions
Exam 13: Techniques of Integration50 Questions
Exam 14: Functions of Several Variables92 Questions
Exam 15: Trigonometric Functions Web60 Questions
Exam 16: Series and Taylor Polynomials Web127 Questions
Exam 17: Probability Web89 Questions
Select questions type
Sketch the graph of the function below. Choose a scale that allows all relative extrema and points of inflection to be identified on the graph.
Free
(Multiple Choice)
4.8/5  (33)
(33)
Correct Answer:
A
p is in dollars and q is the number of units. Find the elasticity of the demand function at the price .
Free
(Multiple Choice)
5.0/5  (36)
(36)
Correct Answer:
C
Compare dy and for at x = 2 with dx = -0.07. Give your answers to four decimal places.
Free
(Multiple Choice)
4.8/5  (30)
(30)
Correct Answer:
B
A power station is on one side of a river that is 0.5 mile wide, and a factory is 6.00 miles downstream on the other side of the river. It costs 18 per foot to run overland power lines and 25 per foot to run underwater power lines. Estimate the value of x that minimizes the cost.
(Multiple Choice)
4.8/5  (30)
(30)
Analytically determine the location(s) of any vertical asymptote(s).
(Multiple Choice)
4.8/5  (26)
(26)
The variable cost for the production of a calculator is 14.25 and the initial investment is 550,000. Use differentials to approximate the change in the cost C for a one-unit increase in production when , where x is the number of units produced.
(Multiple Choice)
4.8/5  (27)
(27)
Find the dimensions of the rectangle of maximum area bounded by the x-axis and y-axis and the graph of . 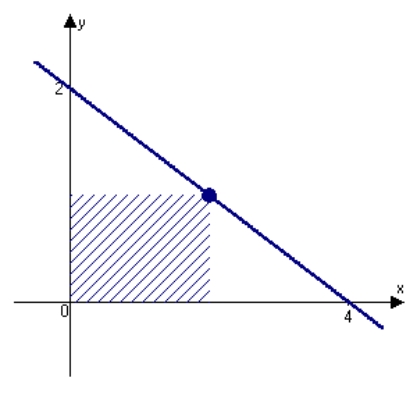
(Multiple Choice)
4.8/5  (38)
(38)
If the total revenue function for a blender is find the maximum revenue.
(Multiple Choice)
4.9/5  (26)
(26)
Sketch the graph of the function using any extrema, intercepts, symmetry, and asymptotes.
(Multiple Choice)
4.9/5  (34)
(34)
A firm can produce 100 units per week. If its total cost function is dollars, and its total revenue function is dollars, how many units x should it produce to maximize its profit?
(Multiple Choice)
4.9/5  (41)
(41)
Analytically determine the location(s) of any horizontal asymptote(s).
(Multiple Choice)
4.7/5  (32)
(32)
The cost C (in millions of dollars) for the federal government to seize p% of a type of illegal drug as it enters the country is modeled by , for . Find the limit of C as .
(Multiple Choice)
4.9/5  (30)
(30)
Average costs. Suppose the average costs of a mining operation depend on the number of machines used, and average costs, in dollars, are given by , where x is the number of machines used. How many machines give minimum average costs?
(Multiple Choice)
4.9/5  (38)
(38)
Showing 1 - 20 of 83
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)