Exam 8: Limits and Derivatives
Exam 1: Fundamental Concepts of Algebra119 Questions
Exam 2: Equations and Inequalities94 Questions
Exam 3: Functions and Graphs96 Questions
Exam 4: Polynomial and Rational Functions105 Questions
Exam 5: Exponential and Logarithmic Functions94 Questions
Exam 6: Systems of Equations and Inequalities96 Questions
Exam 7: Matrices and Determinants94 Questions
Exam 8: Limits and Derivatives77 Questions
Exam 9: Applications of the Derivative83 Questions
Exam 10: Further Applications of the Derivative83 Questions
Exam 11: Derivatives of Exponential and Logarithmic Functions121 Questions
Exam 12: Integration and Its Applications74 Questions
Exam 13: Techniques of Integration50 Questions
Exam 14: Functions of Several Variables92 Questions
Exam 15: Trigonometric Functions Web60 Questions
Exam 16: Series and Taylor Polynomials Web127 Questions
Exam 17: Probability Web89 Questions
Select questions type
When the price of a glass of lemonade at a lemonade stand was $1.75, 400 glasses were sold. When the price was lowered to $1.50, 500 glasses were sold. Assume that the demand function is linear and that the marginal and fixed costs are $0.10 and $ 25, respectively. Find the profit P as a function of x, the number of glasses of lemonade sold.
(Multiple Choice)
4.8/5  (35)
(35)
A graph of is shown and a c-value is given. For this problem, use the graph to find . 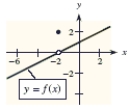
(Multiple Choice)
4.9/5  (26)
(26)
Use the product Rule to find the derivative of the function .
(Multiple Choice)
4.8/5  (36)
(36)
When the price of a glass of lemonade at a lemonade stand was $1.75, 400 glasses were sold. When the price was lowered to $1.50, 500 glasses were sold. Assume that the demand function is linear and that the marginal and fixed costs are $0.10 and $ 25, respectively. Find the marginal profit when 300 glasses of lemonade are sold and when 700 glasses of lemonade are sold.
(Multiple Choice)
4.8/5  (38)
(38)
Find constants a and b such that the function is continuous on the entire real line.
(Multiple Choice)
4.9/5  (39)
(39)
The cost C (in dollars) of producing x units of a product is given by . Find the additional cost when the production increases from 9 t o10.
(Multiple Choice)
4.8/5  (46)
(46)
Find the derivative of the given function. Simplify and express the answer using positive exponents only. 
(Multiple Choice)
4.8/5  (36)
(36)
Find the point(s), if any, at which the graph of f has a horizontal tangent line.
(Multiple Choice)
4.8/5  (35)
(35)
Graph the function with a graphing utility and use it to predict the limit. Check your work either by using the table feature of the graphing utility or by finding the limit algebraically.
(Multiple Choice)
4.9/5  (34)
(34)
Find the x-values (if any) at which f(x) is not continuous and identify whether they are removable or nonremovable.
(Multiple Choice)
4.8/5  (42)
(42)
Identify a function that has the given characteristics and then sketch the function.
(Multiple Choice)
4.9/5  (31)
(31)
A population of bacteria is introduced into a culture. The number of bacteria P can be modeled by where t is the time (in hours). Find the rate of change of the population when t = 2.
(Multiple Choice)
4.8/5  (40)
(40)
A deposit of $6500 is made in an account that pays 6% compounded every 3 months. The amount in the account after years is , t . What are the points of discontinuity of graph of ? (Here, the brackets indicate the greatest integer function.)
(Multiple Choice)
4.9/5  (38)
(38)
Showing 41 - 60 of 77
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)