Exam 7: Matrices and Determinants
Exam 1: Fundamental Concepts of Algebra119 Questions
Exam 2: Equations and Inequalities94 Questions
Exam 3: Functions and Graphs96 Questions
Exam 4: Polynomial and Rational Functions105 Questions
Exam 5: Exponential and Logarithmic Functions94 Questions
Exam 6: Systems of Equations and Inequalities96 Questions
Exam 7: Matrices and Determinants94 Questions
Exam 8: Limits and Derivatives77 Questions
Exam 9: Applications of the Derivative83 Questions
Exam 10: Further Applications of the Derivative83 Questions
Exam 11: Derivatives of Exponential and Logarithmic Functions121 Questions
Exam 12: Integration and Its Applications74 Questions
Exam 13: Techniques of Integration50 Questions
Exam 14: Functions of Several Variables92 Questions
Exam 15: Trigonometric Functions Web60 Questions
Exam 16: Series and Taylor Polynomials Web127 Questions
Exam 17: Probability Web89 Questions
Select questions type
The area of a triangle with vertices and can be given as the absolute value of the determinant Use this formula to find the area of each triangle whose coordinates are and
(Multiple Choice)
4.9/5  (40)
(40)
Use a determinant to find the area of the triangle shown below. 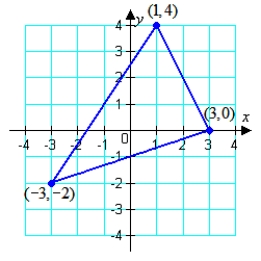
(Multiple Choice)
4.9/5  (45)
(45)
Use the matrix capabilities of a graphing utility to find the inverse of the matrix (if it exists).
(Multiple Choice)
4.7/5  (34)
(34)
Write the augmented matrix for the system of linear equations.
(Multiple Choice)
4.8/5  (34)
(34)
Given , use to decode the following cryptogram: -355 60 -35 -185 15 -25 60 -95 -40 60 -30 10 -145 70 45 -255 90 45 -5 25 45
(Multiple Choice)
4.8/5  (36)
(36)
Two competing companies offer cable television to a city with 100,000 households. Gold Cable Company has 10,000 subscribers and Galaxy Cable Company has 15,000 subscribers. The percent changes in cable subscriptions each year are shown in the matrix below where the columns are percent changes from Gold, from Galaxy, and from Nonsubscriber respectively and the rows are percent changes to Gold, to Galaxy, and to Nonsubscriber respectively. Find the number of nonsubscribers in two years using matrix multiplication.
(Multiple Choice)
4.9/5  (31)
(31)
Solve the system of equations below by the Gaussian elimination method.
(Multiple Choice)
5.0/5  (32)
(32)
Determine whether the two systems of linear equations yield the same solutions. If so, find the solutions using matrices.
(Multiple Choice)
4.8/5  (37)
(37)
An augmented matrix that represents a system of linear equations (in variables x, y, and z) has been reduced using Gauss-Jordan elimination. Write the solution represented by the augmented matrix.
(Multiple Choice)
4.8/5  (35)
(35)
Showing 21 - 40 of 94
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)