Exam 2: Limits and the Derivative
Exam 1: Functions and Graphs71 Questions
Exam 2: Limits and the Derivative188 Questions
Exam 3: Additional Derivative Topics98 Questions
Exam 4: Graphing and Optimization126 Questions
Exam 5: Integration38 Questions
Exam 7: Multivariable Calculus92 Questions
Exam 8: Appendix A: Basic Algebra Review44 Questions
Exam 9: Appendix B: Special Topics Online at Googlmjbxrg20 Questions
Select questions type
Use a calculator to evaluate the expression. Round the result to five decimal places.
-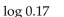
(Multiple Choice)
4.8/5  (40)
(40)
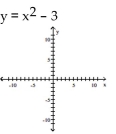
Use point-by-point plotting to sketch the graph of the equation.
-
(Multiple Choice)
4.8/5  (36)
(36)
Solve the problem.
-U. S. Census Bureau data shows that the number of families in the United States (in millions) in year x is given by h(x) 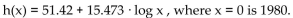 980. How many families were there in 2002?
980. How many families were there in 2002?
(Multiple Choice)
4.9/5  (33)
(33)
Solve the problem.
-The financial department of a company that manufactures portable MP3 players arrived at the following daily
cost equation for manufacturing x MP3 players per day: per day: 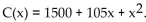 The average cost per unit at The average cost per unit at a
production level of players per day is per day is
The average cost per unit at The average cost per unit at a
production level of players per day is per day is 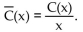 (A) Find the rational function
(A) Find the rational function 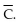 (B) Graph the average cost function on a graphing utility for Graph the average cost function on a graphing utility for 10
(B) Graph the average cost function on a graphing utility for Graph the average cost function on a graphing utility for 10 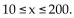 (C) Use the appropriate command on a graphing utility to find the daily production level (to the nearest integer) at
which the average cost per player is a minimum. What is the minimum average cost (to the nearest cent)?
(C) Use the appropriate command on a graphing utility to find the daily production level (to the nearest integer) at
which the average cost per player is a minimum. What is the minimum average cost (to the nearest cent)?
(Essay)
4.9/5  (40)
(40)
For the polynomial function find the following: (i) Degree of the polynomial; (ii) All x intercepts; (iii) The y intercept.
-y = (x + 10)(x + 6)(x + 6)
(Multiple Choice)
4.7/5  (47)
(47)
Solve the problem.
-A carbon-14 dating test is performed on a fossil bone, and analysis finds that 15.5% of the original amount of carbon-14 is still present in the bone. Estimate the age of the fossil bone. (Recall that carbon-14 decays
According to the equation 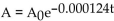 )).
)).
(Multiple Choice)
4.8/5  (30)
(30)
Solve the problem.
-In North America, coyotes are one of the few species with an expanding range. The future population of coyotes in a region of Mississippi valley can be modeled by the equation P = 59 + 12 · ln(18t + 1), where t is time in
Years. Use the equation to determine when the population will reach 170. (Round your answer to the nearest
Tenth year.)
(Multiple Choice)
4.7/5  (32)
(32)
Provide an appropriate response.
-Let T be the set of teachers at a high school and let S be the set of students enrolled at that school. Determine which of
the following correspondences define a function. Explain.
(A) A student corresponds to the teacher if the student is enrolled in the teacher's class.
(B) A student corresponds to every teacher of the school.
(Essay)
4.8/5  (39)
(39)
Provide an appropriate response.
-The following graph represents the result of applying a sequence of transformations to the graph of a basic
function. Identify the basic function and describe the transformation(s). Write the equation for the given graph. 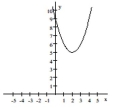
(Essay)
4.8/5  (43)
(43)
Determine whether the relation represents a function. If it is a function, state the domain and range.
-{(-3, 10), (-2, 5), (0, 1), (2, 5), (4, 17)}
(Multiple Choice)
4.8/5  (41)
(41)
Solve the problem.
-Book sales on the Internet (in billions of dollars) in year x are approximated by f(x) = 1.84 + 2.1 · ln x, where x = 0 corresponds to 2000. How much will be spent on Internet book sales in 2008? Round to the nearest tenth.
(Multiple Choice)
4.7/5  (29)
(29)
Determine whether the function is linear, constant, or neither
-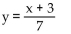
(Multiple Choice)
4.9/5  (36)
(36)
For the given function, find each of the following:
(A) Intercepts
(B) Vertex
(C) Maximum or minimum
(D) Range
-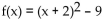
(Multiple Choice)
5.0/5  (39)
(39)
Showing 41 - 60 of 188
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)