Exam 2: Limits and the Derivative
Exam 1: Functions and Graphs71 Questions
Exam 2: Limits and the Derivative188 Questions
Exam 3: Additional Derivative Topics98 Questions
Exam 4: Graphing and Optimization126 Questions
Exam 5: Integration38 Questions
Exam 7: Multivariable Calculus92 Questions
Exam 8: Appendix A: Basic Algebra Review44 Questions
Exam 9: Appendix B: Special Topics Online at Googlmjbxrg20 Questions
Select questions type
Solve the problem.
-The function M described by M(x) = 2.89x + 70.64 can be used to estimate the height, in centimeters, of a male whose humerus (the bone from the elbow to the shoulder) is x cm long. Estimate the height of a male whose
Humerus is 30.93 cm long. Round your answer to the nearest four decimal places.
(Multiple Choice)
4.8/5  (39)
(39)
Solve the problem.
-To estimate the ideal minimum weight of a woman in pounds multiply her height in inches by 4 and subtract 130. Let W = the ideal minimum weight and h = height. Express W as a linear function of h.
(Multiple Choice)
4.8/5  (42)
(42)
Compute and simplify the difference quotient quotient 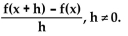 -f(x) = 5
-f(x) = 5 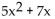
(Multiple Choice)
5.0/5  (35)
(35)
Solve the problem.
-A sample of 800 grams of radioactive substance decays according to the function A(t) = 800e-0.028t, where t is the time in years. How much of the substance will be left in the sample after 10 years? Round to the nearest
Whole gram.
(Multiple Choice)
4.8/5  (37)
(37)
Solve the problem.
-If $1250 is invested at a rate of f 8 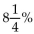 compounded monthly, what is the balance after 10 years?
compounded monthly, what is the balance after 10 years? 
(Multiple Choice)
4.8/5  (39)
(39)
Solve the problem.
-The financial department of a company that produces digital cameras arrived at the following price-demand
function and the corresponding revenue function: 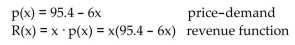 The function p(x) is the wholesale price per camera at which x million cameras can be sold and R(x) is the corresponding
revenue (in million dollars). Both functions have domain 1
The function p(x) is the wholesale price per camera at which x million cameras can be sold and R(x) is the corresponding
revenue (in million dollars). Both functions have domain 1 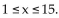 15. They also found the cost function to be C(x) = 150
+ 15.1x (in million dollars) for manufacturing and selling x cameras. Find the profit function and determine the
approximate number of cameras, rounded to the nearest hundredths, that should be sold for maximum profit.
15. They also found the cost function to be C(x) = 150
+ 15.1x (in million dollars) for manufacturing and selling x cameras. Find the profit function and determine the
approximate number of cameras, rounded to the nearest hundredths, that should be sold for maximum profit.
(Essay)
4.9/5  (34)
(34)
Solve graphically to two decimal places using a graphing calculator.
-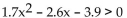
(Multiple Choice)
4.8/5  (42)
(42)
Use the REGRESSION feature on a graphing calculator.
-A strain of E-coli Beu-recA441 is placed into a petri dish at 30°Celsius and allowed to grow. The following data are collected. Theory states that the number of bacteria in the petri dish will initially grow according to the law
Of uninhibited growth. The population is measured using an optical device in which the amount of light that
Passes through the petri dish is measured. 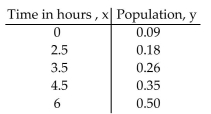 Find the exponential equation in the form rm
Find the exponential equation in the form rm 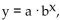 , where x i, where x s the hours of growth. Round to four decimal
Places.
, where x i, where x s the hours of growth. Round to four decimal
Places.
(Multiple Choice)
4.9/5  (39)
(39)
Solve the problem.
-In economics, functions that involve revenue, cost and profit are used. Suppose R(x) and C(x) denote the total revenue and the total cost, respectively, of producing a new high-tech widget. The difference P(x) = R(x) - C(x)
Represents the total profit for producing x widgets. Given x widgets. Given 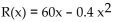 and C(x) = 3x + 13, find the
Equation for P(x).
and C(x) = 3x + 13, find the
Equation for P(x).
(Multiple Choice)
5.0/5  (40)
(40)
Use a calculator to evaluate the expression. Round the result to five decimal places.
-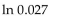
(Multiple Choice)
4.8/5  (32)
(32)
Solve the problem.
-Assume that a person's critical weight W, defined as the weight above which the risk of death rises dramatically, is given by 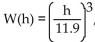 , where W , where W is in pounds and h is the person's height in inches.
Find the tcritical weight for a person who is 6 ft 11 in. tall. Round to the nearest tenth.
, where W , where W is in pounds and h is the person's height in inches.
Find the tcritical weight for a person who is 6 ft 11 in. tall. Round to the nearest tenth.
(Multiple Choice)
4.8/5  (37)
(37)
Showing 121 - 140 of 188
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)