Exam 2: Limits and the Derivative
Exam 1: Functions and Graphs71 Questions
Exam 2: Limits and the Derivative188 Questions
Exam 3: Additional Derivative Topics98 Questions
Exam 4: Graphing and Optimization126 Questions
Exam 5: Integration38 Questions
Exam 7: Multivariable Calculus92 Questions
Exam 8: Appendix A: Basic Algebra Review44 Questions
Exam 9: Appendix B: Special Topics Online at Googlmjbxrg20 Questions
Select questions type
Solve the problem.
-The function F described by F(x) = 2.75x + 71.48 can be used to estimate the height, in centimeters, of a woman whose humerus (the bone from the elbow to the shoulder) is x cm long. Estimate the height of a woman whose
Humerus is 30.93 cm long. Round your answer to the nearest four decimal places.
(Multiple Choice)
4.9/5  (34)
(34)
Find the vertex form for the quadratic function. Then find each of the following:
(A) Intercepts
(B) Vertex
(C) Maximum or minimum
(D) Range
-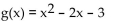
(Multiple Choice)
4.7/5  (38)
(38)
Provide an appropriate response.
-Only one of the following functions has domain which is not equal to all real numbers. State which function and state its
domain.
(A) h(x) 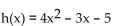 (B)
(B) 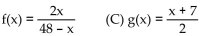
(Essay)
4.8/5  (49)
(49)
Solve the problem.
-Since life expectancy has increased in the last century, the number of Alzheimer's patients has increased dramatically. The number of patients in the United States reached 4 million in 2000. Using data collected since
2000, it has been found that the data can be modeled by the exponential function l function  where
X is the years since 2000. Estimate the Alzheimer's patients in 2025. Round to the nearest tenth.
where
X is the years since 2000. Estimate the Alzheimer's patients in 2025. Round to the nearest tenth.
(Multiple Choice)
4.9/5  (33)
(33)
Determine whether the relation represents a function. If it is a function, state the domain and range.
-{(41, -3), (5, -2), (5, 0), (9, 2), (21, 4)}
(Multiple Choice)
4.8/5  (39)
(39)
Solve the problem.
-A retail chain sells washing machines. The retail price p(x) (in dollars) and the weekly demand x for a particular model are related by the function 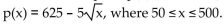 . (i) Describe how the graph of the
Function p can be obtained from the graph of one of the six basic functions: y
. (i) Describe how the graph of the
Function p can be obtained from the graph of one of the six basic functions: y 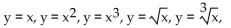 or y = x . (ii) Sketch a graph of function p using part (i) as an aid.
or y = x . (ii) Sketch a graph of function p using part (i) as an aid. 
(Multiple Choice)
4.9/5  (38)
(38)
Determine if the equation specifies a function with independent variable x. If so, find the domain. If not, find a value of x
to which there corresponds more than one value of y.
-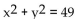
(Multiple Choice)
4.8/5  (35)
(35)
Find the vertex form for the quadratic function. Then find each of the following:
(A) Intercepts
(B) Vertex
(C) Maximum or minimum
(D) Range
-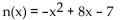
(Multiple Choice)
4.9/5  (30)
(30)
Solve the problem.
-The U. S. Census Bureau compiles data on population. The population (in thousands) of a southern city can be approximated by P(x) 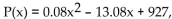 927, where x c where x or responds to the years after 1950. In what calendar
Year was the population about 804,200?
927, where x c where x or responds to the years after 1950. In what calendar
Year was the population about 804,200?
(Multiple Choice)
4.8/5  (36)
(36)
Graph the function.
-Assume it costs 25 cents to mail a letter weighing one ounce or less, and then 20 cents for each additional ounce or fraction of an ounce. Let L(x) be the cost of mailing a letter weighing x ounces. Graph y = L(x). Use the
Interval (0, 4].
(Multiple Choice)
4.7/5  (39)
(39)
For the following problem, (i) graph f and g in the same coordinate system; (ii) solve f(x) = g(x) algebraically to two
decimal places; (iii) solve f(x) > g(x) using parts i and ii; (iv) solve f(x) < g(x) using parts i and ii.
-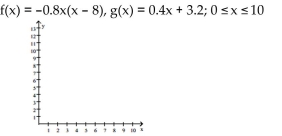
(Multiple Choice)
5.0/5  (32)
(32)
Provide an appropriate response.
-How can the graph of 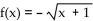 be obtained from be obtained from the graph of
be obtained from be obtained from the graph of 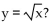
(Multiple Choice)
4.9/5  (36)
(36)
Provide an appropriate response.
-What is the maximum number of x intercepts that a polynomial of degree 10 can have?
(Multiple Choice)
4.7/5  (34)
(34)
Solve the problem.
-In the table below, the amount of the U.S. minimum wage is listed for selected years. 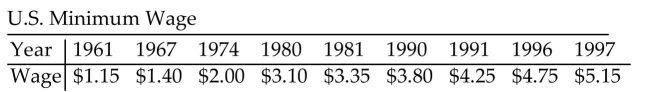 Find an exponential regression model of the form he form y
Find an exponential regression model of the form he form y 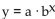 , where y, where y represents the U.S. minimum wage x years
after 1960. Round a and b to four decimal places. According to this model, what will the minimum wage be in
2005? In 2010?
, where y, where y represents the U.S. minimum wage x years
after 1960. Round a and b to four decimal places. According to this model, what will the minimum wage be in
2005? In 2010?
(Essay)
4.8/5  (35)
(35)
Showing 141 - 160 of 188
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)