Exam 8: Linear Optimization Models

Hire-a-Car System rents three types of cars at two different locations. The profit made per day for each car type and company at the two locations is listed below: 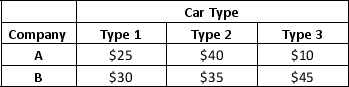The management forecasts the demand per day by car type. A linear programming model developed to maximize profit is used to determine how many reservations to accept for each type of car. The demand forecast for a particular day is 125 rentals for Type 1 cars, 55 rentals for Type 2 cars, and 40 rentals for Type 3 cars. The company has 100 cars in location A and 120 cars in location B. Use linear programming to determine how many reservations to accept for each car type and how the reservations should be allocated to the different locations. Is the demand for any car type not satisfied? Explain.

Free

(Essay)

4.8/5

(34)

Question 1

Correct Answer:

Verified

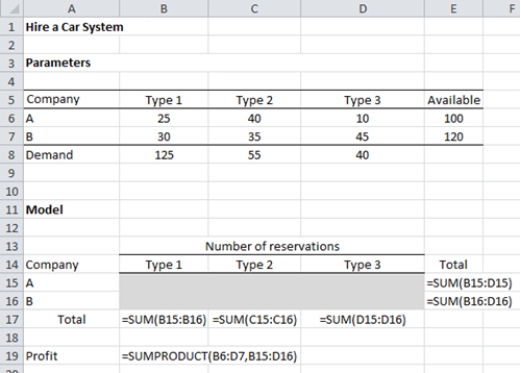
Let A₁ = number of reservations made for Type 1 car of Company A
A₂ = number of reservations made for Type 2 car of Company A
A₃ = number of reservations made for Type 3 car of Company A
B₁ = number of reservations made for Type 1 car of Company B
B₂ = number of reservations made for Type 2 car of Company B
B₃ = number of reservations made for Type 3 car of Company B
Max 25A₁ + 40A₂ + 10A₃ + 30B₁ + 35B₂ + 45B₃
s.t.
A₁ + A₂ + A₃ ≤ 100
B₁ + B₂ + B₃ ≤ 120
A₁ + B₁ ≤ 125
A₂ + B₂ ≤ 55
A₃ + B₃ ≤ 40
A₁, A₂, …, B₃ ≥ 0

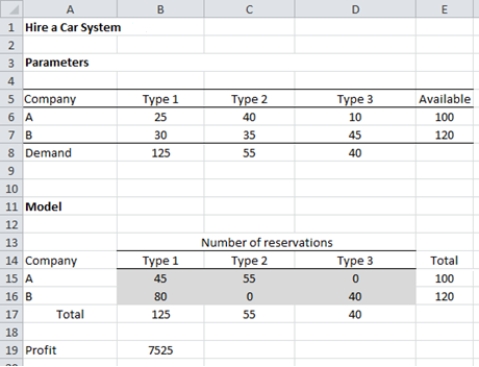
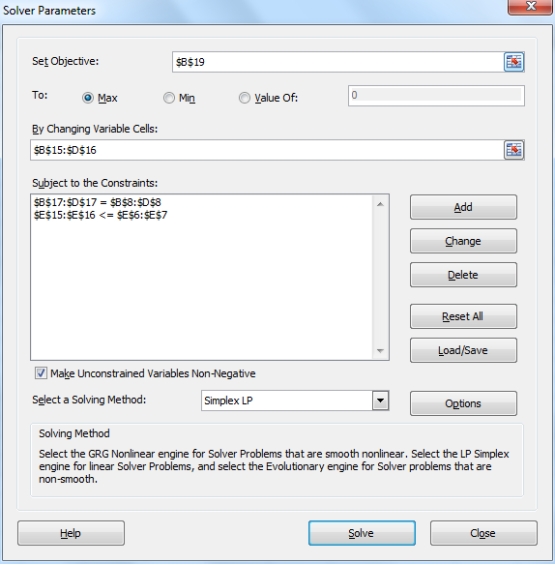The optimal solution obtained using Excel Solver shows the reservations to accept for each car type and their allocation to different locations. Also, the demand for all the car types is satisfied.

A(n) _____ solution satisfies all the constraint expressions simultaneously.

Free

(Multiple Choice)

4.9/5

(27)

Question 2

Correct Answer:

Verified

Jackson just obtained $240,000 by selling mutual funds and is now looking for other investment opportunities for these funds. His financial consultant recommends that all new investments be made in the stocks of industries such as like Agriculture, Healthcare, Banking, Manufacturing, and Real Estate. The projected annual rates of returns for the investments are as follows: 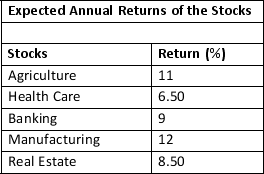His consultant has set constraints on the investments based on the calculated risks involved with the industries: 1) Neither Agriculture nor Manufacturing industry should receive more than $100,000. 2) Neither Healthcare nor Banking should receive more than $50,000. 3) The amount invested in Manufacturing industry should not be more than 45 percent of the sum of the investment in Banking and Healthcare sectors. 4) The amount invested in Real Estate should be at least 20 percent of the sum of the investment in Banking and Healthcare sectors. What portfolio recommendations-investments and amounts-should be made for the available $240,000?

Free

(Essay)

4.9/5

(40)

Question 3

Correct Answer:

Verified

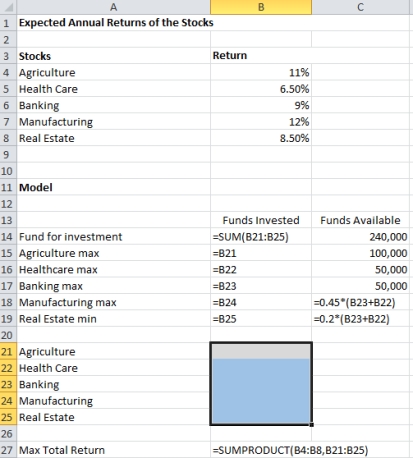
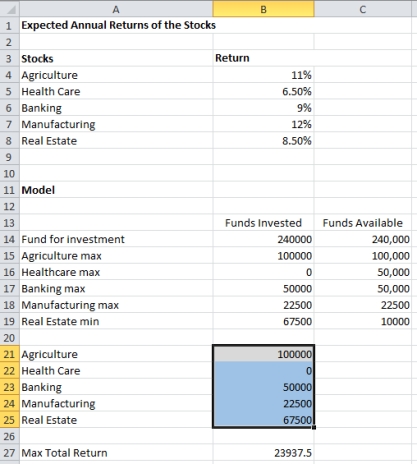
Let X₁ = amount invested in Agriculture
X₂ = amount invested in Health Care
X₃ = amount invested in Banking
X₄ = amount invested in Manufacturing
X₅ = amount invested in Real Estate
Max: 0.11X₁ + 0.065X₂ + 0.09X₃ + 0.12X₄ + 0.085X₅
s.t.
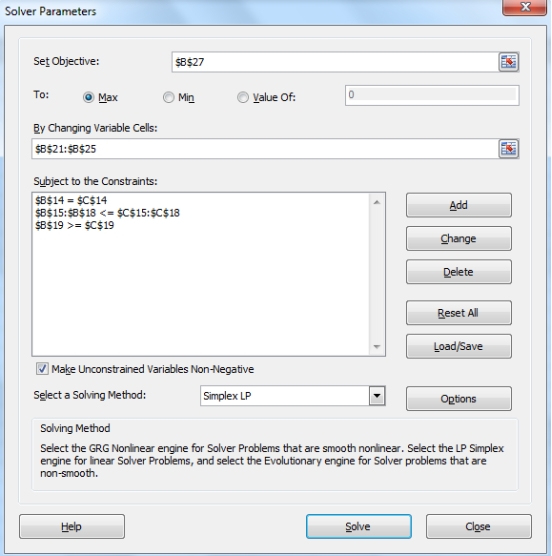
X₁ + X₂ + X₃ + X₄ + X₅ = 240,000
X₁ ≤ 100000
X₄ ≤ 100000
X₂ ≤ 50000
X₃ ≤ 50000
X₄ ≤ 0.45(X₂ + X₃)
X₅ ≥ 0.20(X₂ + X₃)
X₁, X₂, X₃, X₄, X₅ ≥ 0

_____ is the process of translating a verbal statement of a problem into a mathematical statement.

(Multiple Choice)

4.8/5

(25)

Question 4

In a linear programming model, the _____ assumption plus the nonnegativity constraints mean that decision variables can take on any value greater than or equal to zero.

(Multiple Choice)

4.8/5

(34)

Question 5

_____ is an Excel tool that utilizes Dantzig's simplex algorithm to solve linear programs by systematically finding which set of constraints form the optimal extreme point of the feasible region.

(Multiple Choice)

4.7/5

(39)

Question 6

The situation in which the value of the solution may be made infinitely large in a maximization linear programming problem or infinitely small in a minimization problem without violating any of the constraints is known as _____.

(Multiple Choice)

4.8/5

(33)

Question 7

The reduced cost indicates the change in the optimal objective function value that results from changing the right-hand side of the nonnegativity constraint from:

(Multiple Choice)

4.8/5

(37)

Question 8

In the case of a linear model with two decision variables, if the constraints are in the form of inequalities they are visually represented by regions called as:

(Multiple Choice)

4.7/5

(31)

Question 9

In linear programming models of real problems, the occurrence of an unbounded solution means that the:

(Multiple Choice)

4.8/5

(35)

Question 10

The _____ Report generated by Excel Solver gives information on the objective function value when variables are set to their limits.

(Multiple Choice)

4.9/5

(37)

Question 11

The intersections of half spaces represent_____.

(Multiple Choice)

4.8/5

(35)

Question 12

_____ is the situation in which no solution to the linear programming problem satisfies all the constraints.

(Multiple Choice)

5.0/5

(33)

Question 13

When formulating a constraint, care must be taken to ensure that:

(Multiple Choice)

4.7/5

(44)

Question 14

The points where constraints intersect on the boundary of the feasible region are termed as _____.

(Multiple Choice)

4.9/5

(37)

Question 15

The supervisor of a production company is trying to determine the number of two assembling parts, Part X and Part Y to be produced per day in three different sections of the plant. The time required for the production along with the profit contribution for each part are given in the following table: Each part made (X and Y) must be processed in each of the three sections. No more than 60 units of Part X can be produced, but up to 70 units of Part Y can be produced per day. The company already has orders for 30 units of Part Y that must be satisfied. a. Develop a linear programming model and solve the model to determine the optimal production quantities of parts X and Y. b. If more time could be made available in Section 2, how much worth would it be?

(Essay)

4.8/5

(37)

Question 16

A _____ refers to a constraint that holds as equality at the optimal solution.

(Multiple Choice)

5.0/5

(36)

Question 17

Geometrically, binding constraints intersect to form the _____.

(Multiple Choice)

4.9/5

(25)

Question 18

A mathematical function in which each variable appears in a separate term and is raised to the first power is known as a _____.

(Multiple Choice)

4.9/5

(35)

Question 19

Reference - 8.1: Use the information given below to answer questions Rob is a financial manager with Sharez, an investment advisory company. He must select specific investments-for example, stocks and bonds-from a variety of investment alternatives. -Reference - 8.1. Which of the following statements is most likely to be the objective function in this scenario?

(Multiple Choice)

4.8/5

(31)

Question 20

Showing 1 - 20 of 60

A(n) _____ solution satisfies all the constraint expressions simultaneously.

_____ is the process of translating a verbal statement of a problem into a mathematical statement.

In a linear programming model, the _____ assumption plus the nonnegativity constraints mean that decision variables can take on any value greater than or equal to zero.

_____ is an Excel tool that utilizes Dantzig's simplex algorithm to solve linear programs by systematically finding which set of constraints form the optimal extreme point of the feasible region.

The situation in which the value of the solution may be made infinitely large in a maximization linear programming problem or infinitely small in a minimization problem without violating any of the constraints is known as _____.

The reduced cost indicates the change in the optimal objective function value that results from changing the right-hand side of the nonnegativity constraint from:

In the case of a linear model with two decision variables, if the constraints are in the form of inequalities they are visually represented by regions called as:

In linear programming models of real problems, the occurrence of an unbounded solution means that the:

The _____ Report generated by Excel Solver gives information on the objective function value when variables are set to their limits.

The intersections of half spaces represent_____.

_____ is the situation in which no solution to the linear programming problem satisfies all the constraints.

When formulating a constraint, care must be taken to ensure that:

The points where constraints intersect on the boundary of the feasible region are termed as _____.

A _____ refers to a constraint that holds as equality at the optimal solution.

Geometrically, binding constraints intersect to form the _____.

A mathematical function in which each variable appears in a separate term and is raised to the first power is known as a _____.

Introduction

Descriptive Statistics

Data Visualization

Linear Regression

Time Series Analysis and Forecasting

Data Mining

Spreadsheet Models

Integer Linear Optimization Models

Nonlinear Optimization Models

Monte Carlo Simulation

Decision Analysis

Filters