Question 1

Which of the following is true about the sensitivity analysis for integer optimization problems?

Accepted Answer

A)  Sensitivity reports are readily available for integer optimization problems similar to the linear programming problems. 
B)  Because of the discrete nature of the integer optimization, Excel Solver takes much more time to calculate objective function coefficient ranges, shadow prices, and right-hand-side ranges. 
C)  The sensitivity analysis is not important for integer problems. 
D)  To determine the sensitivity of the solution to changes in model inputs for integer optimization problems, the data must be changed and the problem must be re-solve
D)  
A)  Sensitivity reports are readily available for integer optimization problems similar to the linear programming problems. 
B)  Because of the discrete nature of the integer optimization, Excel Solver takes much more time to calculate objective function coefficient ranges, shadow prices, and right-hand-side ranges. 
C)  The sensitivity analysis is not important for integer problems. 
D)  To determine the sensitivity of the solution to changes in model inputs for integer optimization problems, the data must be changed and the problem must be re-solve
D)  D

Question 2

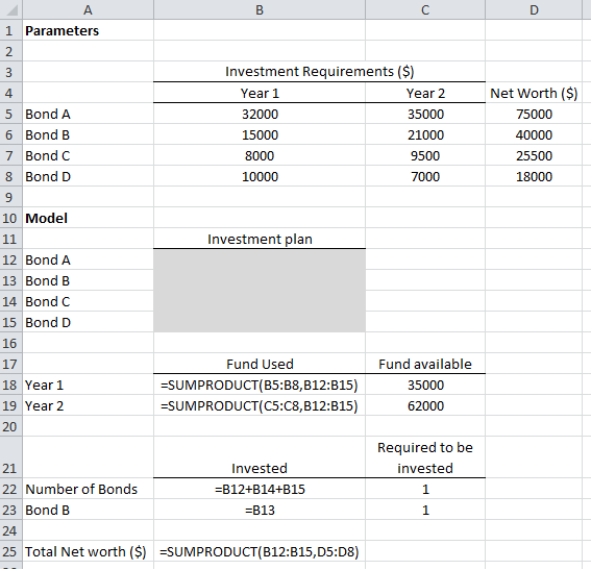
Sansuit Investments is deciding on future investment for the coming two years. The company considered four bonds to choose from and their investment details for the next two years are given in the table below:
   
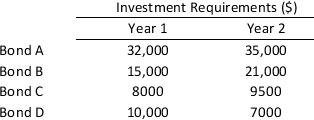The net worth of these four bonds is $75,000, $40,000, $25,500, and $18,000, respectively. The funds available with the company for Year 1 and Year 2 are $35,000 and $62,000, respectively. a. Develop and solve a binary integer programming model for maximizing the net worth assuming that only one of the bonds can be considered.
b. Suppose the investment has to be made on Bond B, and only two of the four bonds can be considered for investment. Modify your formulation from part a. to reflect this new situation. Of these two options, which is better?

Accepted Answer

a. Let x₁ = 1 if Bond A is selected for investment; 0 if it is not
X₂ = 1 if Bond B is selected for investment; 0 if it is not
X₃ = 1 if Bond C is selected for investment; 0 if it is not
X₄ = 1 if Bond D is selected for investment; 0 if it is not
Max 75000X₁ + 40000X₂ + 25500X₃ + 18000X₄
s.t.
32000X₁ + 15000X₂ + 8000X₃ + 10000X₄ ≤ 35000
35000X₁ + 21000X₂ + 9500X₃ + 7000X₄ ≤ 62000
X₁ + X₂ + X₃ + X₄ = 1
X₁, X₂, X₃, X₄ = 0, 1

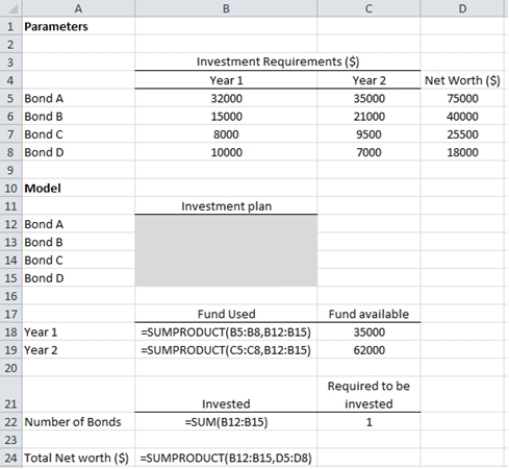
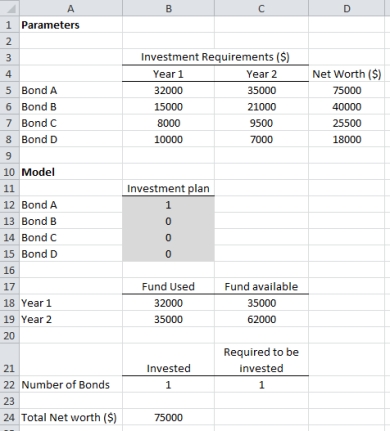
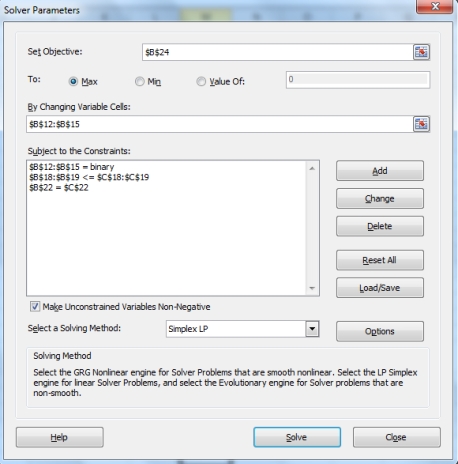
The optimal solution is $75,000.
b. Let x₁ = 1 if Bond A is selected for investment; 0 if it is not
X₂ = 1 if Bond B is selected for investment; 0 if it is not
X₃ = 1 if Bond C is selected for investment; 0 if it is not
X₄ = 1 if Bond D is selected for investment; 0 if it is not
Max 75000X₁ + 40000X₂ + 25500X₃ + 18000X₄
s.t.
32000X₁ + 15000X₂ + 8000X₃ + 10000X₄ ≤ 35000
35000X₁ + 21000X₂ + 9500X₃ + 7000X₄ ≤ 62000
X₂ = 1
X₁ + X₃ + X₄ = 1
X₁, X₂, X₃, X₄ = 0, 1

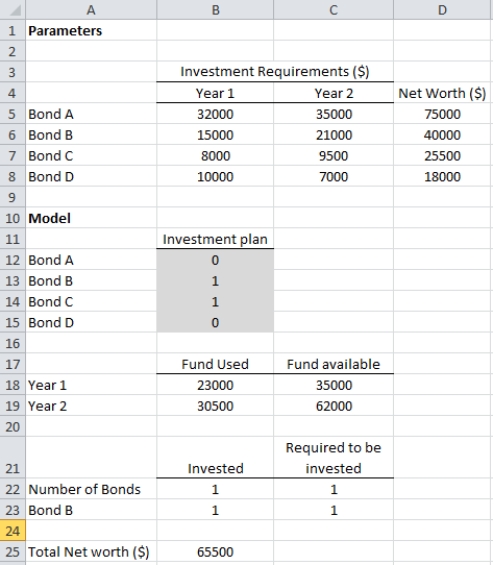
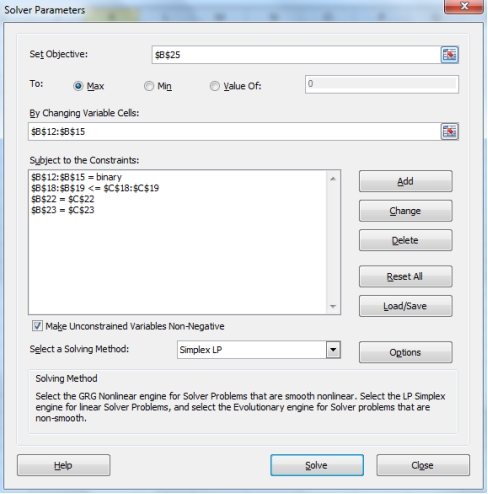Here, the optimal solution is obtained as $65,500 which is less than $75,000, the optimal solution obtained for part a. Hence, the option a. of investing in bonds is better than option b.

Question 3

Reference - 9.1. The levels - small, medium, and large of the size attribute are modeled using:

Accepted Answer

A)  objective function coefficients. 
B)  slack variables. 
C)  binary variables. 
D)  nonlinear coefficients. 
A)  objective function coefficients. 
B)  slack variables. 
C)  binary variables. 
D)  nonlinear coefficients. C

Question 4

In a fixed-cost problem, choosing excessively large values for the maximum production quantity will result in:

Accepted Answer

A)  all reasonable levels of production. 
B)  no production. 
C)  no solution at all. 
D)  possibly a slow solution procedure. 
A)  all reasonable levels of production. 
B)  no production. 
C)  no solution at all. 
D)  possibly a slow solution procedure.

Question 5

_____ is a binary integer programming problem that involves choosing which possible projects or activities provide the best investment return.

Accepted Answer

A)  Capital budgeting problem 
B)  Fixed-cost problem 
C)  Market share optimization problem 
D)  Location problem 
A)  Capital budgeting problem 
B)  Fixed-cost problem 
C)  Market share optimization problem 
D)  Location problem

Question 6

ROFiL Pizza Delivery is planning to open new stores in different other regions so that the excess demand for the pizza home delivery services is met. The locations under consideration and the potential areas (coded in numbers 1-9) that can be reached quickly from the considered locations for home delivery are given in the following table:
   
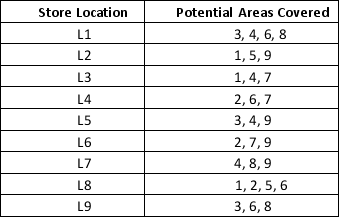Formulate an integer programming model that could be used to find the minimum number of stores to open in order to cover customers of all areas for the home delivery service.

Accepted Answer

Let L₁, L₂, L₃, L₄, L₅, L₆, L₇, L₈, and

Question 7

Which of the following is true of rounding the solution to an integer?

Accepted Answer

A)  It always produces the most optimal integer solution. 
B)  It never produces a feasible solution. 
C)  It does not affect the objective function. 
D)  It may or may not be feasible. 
A)  It always produces the most optimal integer solution. 
B)  It never produces a feasible solution. 
C)  It does not affect the objective function. 
D)  It may or may not be feasible.

Question 8

Greenbell Software Inc. conducted a study on its smartphone products in the market to determine which phone has the best features in terms of three prominent attributes: operating system of the phone (A or B), RAM (512MB or 1GB), and the rear camera specifications (3MP, 5MP, or 7MP) provided with the phone. Eight sample customers have participated in the study and provided the following part-worths for each of the above attributes.
   
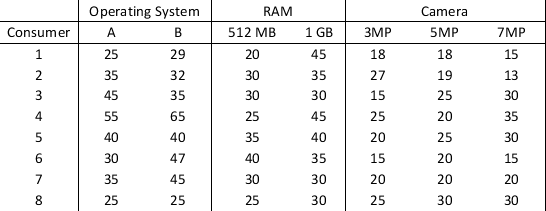Assume the overall utility (sum of part-worths) of the current favorite Greenbell smartphone for customers 1 to 5 is 105 and customers 6 to 8 is 90. What new product design will maximize the share of choice for the eight consumers in the sample?

Accepted Answer

Note: There are alternative optima for t

Question 9

BBest Ink Printing Co. received an order to print a minimum of 50,000 tickets for a concert. They have three printing machines available to meet the order they received. The set-up cost of these machines and the unit cost/ticket printed using each machine along with their maximum production are provided in the table below:
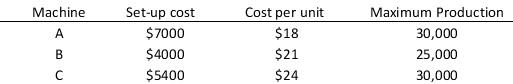   a. Formulate a binary integer linear programming model to find two machines that could be used to print the required number of tickets in order to minimize the cost.
b. Solve the problem in part a.

Accepted Answer

a. Let P1 = Number of tickets printed by

Question 10

Reference - 9.1. The available size of the trousers will be a(n) _____ in an integer programming model for this problem.

Accepted Answer

A)  binary variable 
B)  constraint 
C)  attribute 
D)  regression constant 
A)  binary variable 
B)  constraint 
C)  attribute 
D)  regression constant

Question 11

In binary integer linear program, the integer variables take only the values:

Accepted Answer

A)  0 or 1. 
B)  0 or ∞. 
C)  1 or ∞. 
D)  1 or -1. 
A)  0 or 1. 
B)  0 or ∞. 
C)  1 or ∞. 
D)  1 or -1.

Question 12

Sansuit Investments is deciding on future investment for the coming two years. The company considered four bonds to choose from and their investment details for the next two years are given in the table below:
   
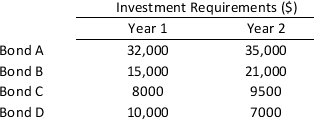The net worth of these four bonds is $75,000, $40,000, $25,500, and $18,000, respectively. The funds available with the company for Year 1 and Year 2 are $35,000 and $62,000, respectively. Develop and solve a binary integer programming model for maximizing the net worth.

Accepted Answer

Let X₁ = 1 if Bond A is selected for inv

Question 13

A manufacturer wants to construct warehouses in six different locations of the city to supply dry cells to his customers on time. The manufacturer wants to construct the minimum number of warehouses, to meet the market demand on time, such that at least one warehouse is within 40 miles from each other warehouse. The following table provides the distance (in miles) between the locations.
   
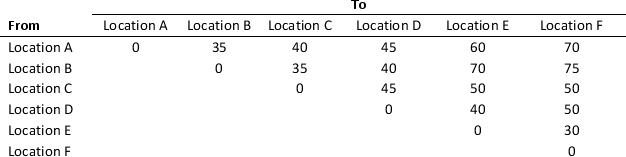Formulate and solve an integer linear program that can be used to determine the minimum number of warehouses needed to be constructed. What are their locations?

Accepted Answer

Let X₁, X₂, X₃, X₄, X₅, and X₆ be the va

Question 14

The worksheet formulation for integer linear programs and linear programming problems is exactly the same except that the _____ for integer linear programs.

Accepted Answer

A)  objective function using Set Objective in the Solver Parameters dialog box is set to Value Of option 
B)  decision variables need not be added in By Changing Variable Cells in the Solver Parameters dialog box 
C)  decision variables must be added in By Changing Variable Cells in the Solver Parameters dialog box along with selecting the Ignore Integer Constraints in the Integer Options dialog box 
D)  constraints must be added in the Solver Parameters dialog box to identify the integer variables and the value for Tolerance in the Integer Options dialog box may need to be adjusted 
A)  objective function using Set Objective in the Solver Parameters dialog box is set to Value Of option 
B)  decision variables need not be added in By Changing Variable Cells in the Solver Parameters dialog box 
C)  decision variables must be added in By Changing Variable Cells in the Solver Parameters dialog box along with selecting the Ignore Integer Constraints in the Integer Options dialog box 
D)  constraints must be added in the Solver Parameters dialog box to identify the integer variables and the value for Tolerance in the Integer Options dialog box may need to be adjusted

Question 15

Andrew is ready to invest $200,000 in stocks and he has been provided nine different alternatives by his financial consultant. The following stocks belong to three different industrial sectors and each sector has three varieties of stocks each with different expected rate of return. The average rate of return taken for the past ten years is provided with each of the nine stocks.
   
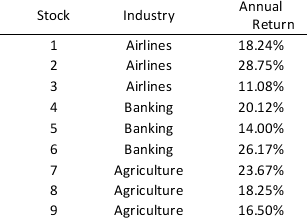The decision will be based on the constraints provided below:
-Exactly 5 alternatives should be chosen.
-One stock can have a maximum invest of $55,000.
-Any stock chosen must have a minimum investment of at least $25,000.
-For the Airlines sector, the maximum number of stocks chosen should be two.
-The total amount invested in Banking must be at least as much as the amount invested in Agriculture.
Now, formulate a model that will decide Andrew's investment strategy to maximize his expected annual return.

Accepted Answer

Let X₁, X₂, X₃, X₄, X₅, X₆, X₇, X₈, and

Question 16

The objective function for a linear optimization problem is: Max 3x + 2y, with one of the constraints being x, y = 0, 1. x and y are the only decision variables. This is an example of a _____.

Accepted Answer

A)  nonlinear program 
B)  mixed-integer linear program 
C)  LP relaxation of the integer linear program 
D)  binary integer linear program 
A)  nonlinear program 
B)  mixed-integer linear program 
C)  LP relaxation of the integer linear program 
D)  binary integer linear program

Question 17

The importance of _____ for integer linear programming problems is often intensified by the fact that a small change in one of the coefficients in the constraints can cause a relatively large change in the value of the optimal solution.

Accepted Answer

A)  objective function 
B)  decision variables 
C)  sensitivity analysis 
D)  optimization analysis 
A)  objective function 
B)  decision variables 
C)  sensitivity analysis 
D)  optimization analysis

Question 18

Reference - 9.1. The part-worths for each of the attribute levels obtained from an initial customer survey and the subsequent regression analysis can be used to determine the:

Accepted Answer

A)  customer utility value. 
B)  optimal solution for the regression analysis. 
C)  overall profit for the company. 
D)  overall sales achieved by the company. 
A)  customer utility value. 
B)  optimal solution for the regression analysis. 
C)  overall profit for the company. 
D)  overall sales achieved by the company.

Question 19

Reference - 9.1. Pink, green, and black will be _____ of the color attribute.

Accepted Answer

A)  levels 
B)  constraints 
C)  regression constants 
D)  utility values 
A)  levels 
B)  constraints 
C)  regression constants 
D)  utility values

Question 20

According to the _____ constraint, the sum of two or more binary variables must be equal to one.

Accepted Answer

A)  conditional 
B)  corequisite 
C)  multiple-choice 
D)  mutually exclusive 
A)  conditional 
B)  corequisite 
C)  multiple-choice 
D)  mutually exclusive

Which of the following is true about the sensitivity analysis for integer optimization problems?

Reference - 9.1. The levels - small, medium, and large of the size attribute are modeled using:

In a fixed-cost problem, choosing excessively large values for the maximum production quantity will result in:

_____ is a binary integer programming problem that involves choosing which possible projects or activities provide the best investment return.

Which of the following is true of rounding the solution to an integer?

Reference - 9.1. The available size of the trousers will be a(n) _____ in an integer programming model for this problem.

In binary integer linear program, the integer variables take only the values:

The worksheet formulation for integer linear programs and linear programming problems is exactly the same except that the _____ for integer linear programs.

The objective function for a linear optimization problem is: Max 3x + 2y, with one of the constraints being x, y = 0, 1. x and y are the only decision variables. This is an example of a _____.

The importance of _____ for integer linear programming problems is often intensified by the fact that a small change in one of the coefficients in the constraints can cause a relatively large change in the value of the optimal solution.

Reference - 9.1. The part-worths for each of the attribute levels obtained from an initial customer survey and the subsequent regression analysis can be used to determine the:

Reference - 9.1. Pink, green, and black will be _____ of the color attribute.

According to the _____ constraint, the sum of two or more binary variables must be equal to one.

Introduction

Descriptive Statistics

Data Visualization

Linear Regression

Time Series Analysis and Forecasting

Data Mining

Spreadsheet Models

Linear Optimization Models

Nonlinear Optimization Models

Monte Carlo Simulation

Decision Analysis

Filters

Exam 9: Integer Linear Optimization Models

Which of the following is true about the sensitivity analysis for integer optimization problems?

Reference - 9.1. The levels - small, medium, and large of the size attribute are modeled using:

In a fixed-cost problem, choosing excessively large values for the maximum production quantity will result in:

_____ is a binary integer programming problem that involves choosing which possible projects or activities provide the best investment return.

Which of the following is true of rounding the solution to an integer?

Reference - 9.1. The available size of the trousers will be a(n) _____ in an integer programming model for this problem.

In binary integer linear program, the integer variables take only the values:

The worksheet formulation for integer linear programs and linear programming problems is exactly the same except that the _____ for integer linear programs.

The objective function for a linear optimization problem is: Max 3x + 2y, with one of the constraints being x, y = 0, 1. x and y are the only decision variables. This is an example of a _____.

The importance of _____ for integer linear programming problems is often intensified by the fact that a small change in one of the coefficients in the constraints can cause a relatively large change in the value of the optimal solution.

Reference - 9.1. The part-worths for each of the attribute levels obtained from an initial customer survey and the subsequent regression analysis can be used to determine the:

Reference - 9.1. Pink, green, and black will be _____ of the color attribute.

According to the _____ constraint, the sum of two or more binary variables must be equal to one.

Introduction

Descriptive Statistics

Data Visualization

Linear Regression

Time Series Analysis and Forecasting

Data Mining

Spreadsheet Models

Linear Optimization Models

Nonlinear Optimization Models

Monte Carlo Simulation

Decision Analysis

Filters