Exam 4: Regression

Tail-feather length in birds is sometimes a sexually dimorphic trait. That is, the trait differs substantially for males and for females. Researchers studied the relationship between tail-feather length (measuring the R1 central tail feather) and weight in a sample of 20 male and 21 female long-tailed finches raised in an aviary. 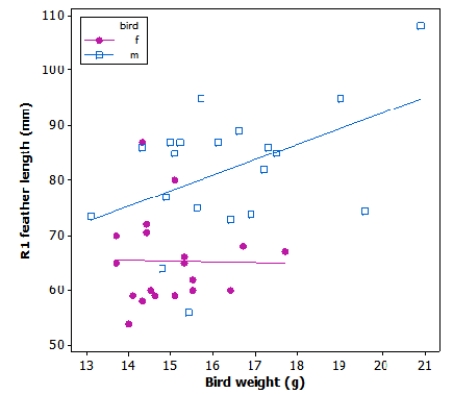Which of the following statements is NOT true?

Tail-feather length in birds is sometimes a sexually dimorphic trait. That is, the trait differs substantially for males and for females. Researchers studied the relationship between weight (x) and tail-feather length (y) in a sample of five wild, male long-tailed finches. Here are the data and software output: weight () tail length () 20.8 82.5 19.1 82.5 15.9 67.0 16.7 70.5 15.7 73.5 Simple linear regression results: Dependent Variable: tail length Independent Variable: weight tail length $= 25.547393 + 2.8147736$ weight Sample size: 5 $R$ (correlation coefficient $) = 0.88813734$ $\mathrm { R } - \mathrm { sq } = 0.78878793$ Estimate of error standard deviation: $3.7411656$ Parameter estimates: Parameter Estimate Std. Err. Alternative DF T-Stat P-value Intercept 25.547393 14.928136 0 3 1.7113585 0.1855 Slope 2.8147736 0.84093435 0 3 3.3471979 0.0442 Approximately what percent of variation in tail-feather length can be explained by weight among male long-tailed finches?

Tail-feather length in birds is sometimes a sexually dimorphic trait. That is, the trait differs substantially for males and for females. Researchers studied the relationship between tail-feather length (measuring the R1 central tail feather) and weight in a sample of 20 male and 21 female long-tailed finches raised in an aviary. 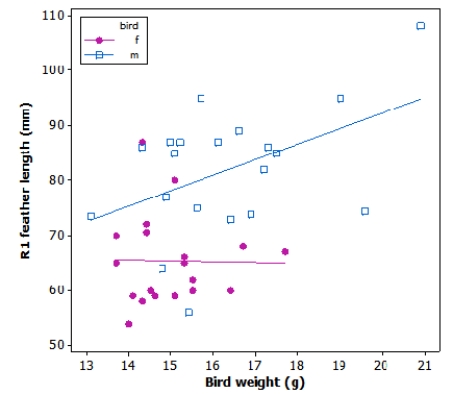What is the approximate value of the slope for the male regression line (blue squares)?

Which of the following statements is correct?

Tail-feather length in birds is sometimes a sexually dimorphic trait. That is, the trait differs substantially for males and for females. Researchers studied the relationship between weight (x) and tail-feather length (y) in a sample of five wild, male long-tailed finches. Here are the data and software output: weight () tail length () 20.8 82.5 19.1 82.5 15.9 67.0 16.7 70.5 15.7 73.5 Simple linear regression results: Dependent Variable: tail length Independent Variable: weight tail length $= 25.547393 + 2.8147736$ weight Sample size: 5 $R$ (correlation coefficient $) = 0.88813734$ $\mathrm { R } - \mathrm { sq } = 0.78878793$ Estimate of error standard deviation: $3.7411656$ Parameter estimates: Parameter Estimate Std. Err. Alternative DF T-Stat P-value Intercept 25.547393 14.928136 0 3 1.7113585 0.1855 Slope 2.8147736 0.84093435 0 3 3.3471979 0.0442 What would be the predicted tail-feather length of a male long-tailed finch weighing 30 g?

Before surgical removal of a diseased parathyroid gland, two tests are often performed: the standard intact test and the turbo test. Both tests measure parathyroid hormone (PTH, in ng/l), but the turbo test is very expensive. Researchers obtained data from both tests in a sample of 48 patients to predict turbo test results (y) from standard intact test results (x). The data ranged from roughly 0 to 500 ng/l, and a scatterplot showed a clear linear relationship. The published findings are summarized exactly as follows: Y = 1.08x - 4.36 (r = 0.97; n = 48) For a PTH level of x = 1000 ng/l with the standard intact test, what is the predicted PTH level with the turbo test?

Tail-feather length in birds is sometimes a sexually dimorphic trait. That is, the trait differs substantially for males and for females. Researchers studied the relationship between tail-feather length (measuring the R1 central tail feather) and weight in a sample of 20 male and 21 female long-tailed finches raised in an aviary. 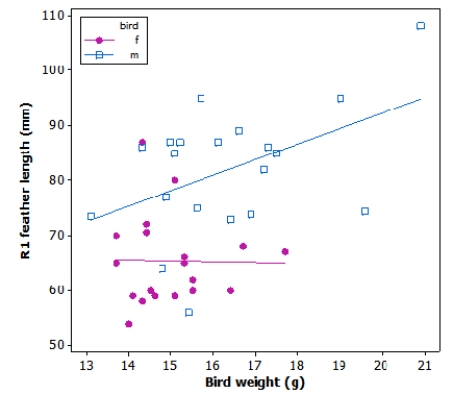What is a meaningful interpretation in context of the estimate of the y intercept of the least squares line for males (blue squares)?

One of nature's patterns connects the percent of adult birds in a colony that return from the previous year and the number of new adults that join the colony. Here are data for 13 colonies of sparrowhawks (a type of bird) and the software output: ? ? Percent return 74 66 81 52 73 62 52 45 62 46 60 46 38 New adults 5 6 8 11 12 15 16 17 18 18 19 20 20 ? Simple linear regression results: Dependent Variable: New adults Independent Variable: percentage return New adults $= 31.934259 - 0.30402295$ percentage return Sample size: 13 $R$ (correlation coefficient $) = - 0.7484673$ $\mathrm { R } - \mathrm { sq } = 0.5602033$ Estimate of error standard deviation: $3.6668913$ Parameter estimates: Parameter Estimate Std. Err. Alternative DF T-Stat p-value Intercept 31.934259 4.8376164 0 11 6.6012383 <0.0001 Slope -0.30402295 0.081220034 0 11 -3.7432014 0.0032 A scatterplot of the data shows that there is a linear relationship between the percent x of adult sparrowhawks that return to a colony from the previous year and the number y of new adult birds that join the colony. What is the least-squares regression line for predicting y from x

Babies typically learn to crawl approximately 6 months after birth. However, it may take longer for babies to learn to crawl in the winter, when they are often bundled in clothes that restrict their movement. Thus, there may be an association between a baby's crawling age and the average temperature during the month they first try to crawl. Below are the average ages (in weeks) at which babies began to crawl for a sample of babies born in each of the 12 months of the year. In addition, the average temperature (in °F) for the month that is 6 months after the birth month is listed. ? ? Birth month Average crawling age Average temperature January 29.84 66 February 30.52 73 March 29.70 72 April 31.84 63 May 28.58 52 June 31.44 39 July 33.64 33 August 32.82 30 September 33.83 33 October 33.35 37 November 33.38 48 December 32.32 57 We want to investigate whether the average age at which infants begin to crawl (y) can be predicted from the average outdoor temperature (x) 6 months after birth, when the babies are likely to begin crawling. We decide to fit a least-squares regression line to the data, with x as the explanatory variable and y as the response variable. We compute the following quantities: R = correlation between x and y = -0.7 X?= mean of the values of x = 50.25 ?= mean of the values of y = 31.77 S_x = standard deviation of the values of x = 15.85 S_y = standard deviation of the values of y = 1.76 Which of the following values is closest to the slope of the least-squares regression line?

A researcher noticed that, for streams along the East Coast, the amount of money spent on restoration and the number of distinct fish populations present appeared to have a negative correlation. The researcher concluded that a lurking variable must be present. What does the researcher mean by a "lurking variable"?

A research survey of approximately 13,900 incoming freshmen in U.S. universities and colleges found that the amount of time a student spends drinking alcohol is a strong predictor of that student's GPA, and that there is a negative association between the two characteristics. Which of the following statements about these results is true?

Tail-feather length in birds is sometimes a sexually dimorphic trait. That is, the trait differs substantially for males and for females. Researchers studied the relationship between tail-feather length (measuring the R1 central tail feather) and weight in a sample of 20 male and 21 female long-tailed finches raised in an aviary. 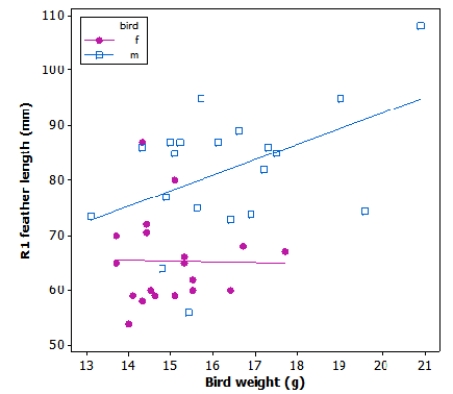We would like to use the observed least-squares regression line between weight and tail-feather length of males to predict the tail-feather length of a male long-tailed finch weighing 28 g. Would this use be appropriate?

Two researchers are interested in the same response variable-namely, the amount of phosphorus present in a particular stream. The first researcher regresses the amount of phosphorus against the amount of total dissolved solids (TDS), giving a slope of 0.327, while the second researcher regresses the amount of phosphorus against specific conductivity (SC) and gets a slope of 2.616. What do these results mean?

A researcher noticed that, for streams along the East Coast, the amount of money spent on restoration and the number of distinct fish populations present appeared to have a negative correlation. Which of the following statements is most likely to be the reasoning the researcher used to decide that a lurking variable must be present?

Babies typically learn to crawl approximately 6 months after birth. However, it may take longer for babies to learn to crawl in the winter, when they are often bundled in clothes that restrict their movement. Thus, there may be an association between a baby's crawling age and the average temperature during the month they first try to crawl. Below are the average ages (in weeks) at which babies began to crawl for a sample of babies born in each of the 12 months of the year. In addition, the average temperature (in °F) for the month that is 6 months after the birth month is listed. ? ? Birth month Average crawling age Average temperature January 29.84 66 February 30.52 73 March 29.70 72 April 31.84 63 May 28.58 52 June 31.44 39 July 33.64 33 August 32.82 30 September 33.83 33 October 33.35 37 November 33.38 48 December 32.32 57 We want to investigate whether the average age at which infants begin to crawl (y) can be predicted from the average outdoor temperature (x) 6 months after birth, when the babies are likely to begin crawling. We decide to fit a least-squares regression line to the data, with x as the explanatory variable and y as the response variable. We compute the following quantities: R = correlation between x and y = -0.7 X?= mean of the values of x = 50.25 ?= mean of the values of y = 31.77 S_x = standard deviation of the values of x = 15.85 S_y = standard deviation of the values of y = 1.76 Suppose that instead of recording the average crawling ages of babies and average temperatures 6 months after their birth, we recorded the actual crawling age of babies and the outdoor temperature exactly 6 months after their birth. Which of the following statements best describes the resulting correlation?

Tail-feather length in birds is sometimes a sexually dimorphic trait. That is, the trait differs substantially for males and for females. Researchers studied the relationship between weight (x) and tail-feather length (y) in a sample of five wild, male long-tailed finches. Here are the data and software output: weight () tail length () 20.8 82.5 19.1 82.5 15.9 67.0 16.7 70.5 15.7 73.5 Simple linear regression results: Dependent Variable: tail length Independent Variable: weight tail length $= 25.547393 + 2.8147736$ weight Sample size: 5 $R$ (correlation coefficient $) = 0.88813734$ $\mathrm { R } - \mathrm { sq } = 0.78878793$ Estimate of error standard deviation: $3.7411656$ Parameter estimates: Parameter Estimate Std. Err. Alternative DF T-Stat P-value Intercept 25.547393 14.928136 0 3 1.7113585 0.1855 Slope 2.8147736 0.84093435 0 3 3.3471979 0.0442 What is the value of the y intercept for the least-squares regression line based on these data?

Tail-feather length in birds is sometimes a sexually dimorphic trait. That is, the trait differs substantially for males and for females. Researchers studied the relationship between tail-feather length (measuring the R1 central tail feather) and weight in a sample of 20 male and 21 female long-tailed finches raised in an aviary. 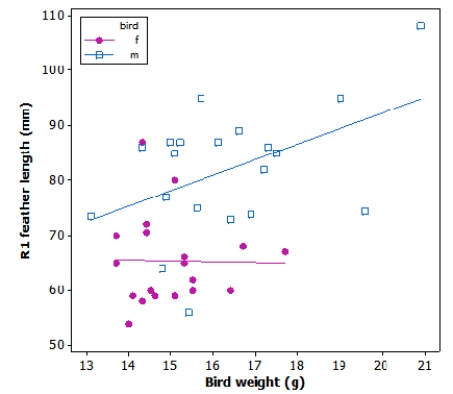We would like to use the observed least-squares regression line between weight and tail-feather length of females to predict the tail-feather length of a male long-tailed finch weighing 8 g. Would this prediction be appropriate?

Babies typically learn to crawl approximately 6 months after birth. However, it may take longer for babies to learn to crawl in the winter, when they are often bundled in clothes that restrict their movement. Thus, there may be an association between a baby's crawling age and the average temperature during the month they first try to crawl. Below are the average ages (in weeks) at which babies began to crawl for a sample of babies born in each of the 12 months of the year. In addition, the average temperature (in °F) for the month that is 6 months after the birth month is listed. ? ? Birth month Average crawling age Average temperature January 29.84 66 February 30.52 73 March 29.70 72 April 31.84 63 May 28.58 52 June 31.44 39 July 33.64 33 August 32.82 30 September 33.83 33 October 33.35 37 November 33.38 48 December 32.32 57 We want to investigate whether the average age at which infants begin to crawl (y) can be predicted from the average outdoor temperature (x) 6 months after birth, when the babies are likely to begin crawling. We decide to fit a least-squares regression line to the data, with x as the explanatory variable and y as the response variable. We compute the following quantities: R = correlation between x and y = -0.7 X?= mean of the values of x = 50.25 ?= mean of the values of y = 31.77 S_x = standard deviation of the values of x = 15.85 S_y = standard deviation of the values of y = 1.76 Which of the following values is closest to the intercept of the least-squares regression line?

Babies typically learn to crawl approximately 6 months after birth. However, it may take longer for babies to learn to crawl in the winter, when they are often bundled in clothes that restrict their movement. Thus, there may be an association between a baby's crawling age and the average temperature during the month they first try to crawl. Below are the average ages (in weeks) at which babies began to crawl for a sample of babies born in each of the 12 months of the year. In addition, the average temperature (in °F) for the month that is 6 months after the birth month is listed. ? ? Birth month Average crawling age Average temperature January 29.84 66 February 30.52 73 March 29.70 72 April 31.84 63 May 28.58 52 June 31.44 39 July 33.64 33 August 32.82 30 September 33.83 33 October 33.35 37 November 33.38 48 December 32.32 57 We want to investigate whether the average age at which infants begin to crawl (y) can be predicted from the average outdoor temperature (x) 6 months after birth, when the babies are likely to begin crawling. We decide to fit a least-squares regression line to the data, with x as the explanatory variable and y as the response variable. We compute the following quantities: R = correlation between x and y = -0.7 X?= mean of the values of x = 50.25 ?= mean of the values of y = 31.77 S_x = standard deviation of the values of x = 15.85 S_y = standard deviation of the values of y = 1.76 Which value gives the fraction of the variation in the values of a response y that is explained by the least-squares regression of y on x?

Suppose you compute the least-squares regression line for a set of data and find that the slope is 91.2. You then remove a point from the data, recompute the least-squares regression line, and find that the new slope is 13.7. What should the removed point be considered?