Exam 16: Dynamic Games With Incomplete Information
Exam 1: Introduction to Game Theory35 Questions
Exam 2: Noncooperative, One-Time, Static Games86 Questions
Exam 3: Focal-Point and Evolutionary Equilibria32 Questions
Exam 4: Infinitely-Repeated, Static Games37 Questions
Exam 5: Finitely-Repeated, Static Games40 Questions
Exam 6: Mixing Pure Strategies51 Questions
Exam 7: Static Games With Continuous Strategies24 Questions
Exam 8: Imperfect Competition52 Questions
Exam 9: Perfect Competition and Monopoly33 Questions
Exam 10: Strategic Trade Policy35 Questions
Exam 11: Dynamic Games With Complete47 Questions
Exam 12: Bargaining54 Questions
Exam 13: Pure Strategies With Uncertain Payoffs65 Questions
Exam 14: Torts and Contracts45 Questions
Exam 15: Auctions44 Questions
Exam 16: Dynamic Games With Incomplete Information34 Questions
Select questions type
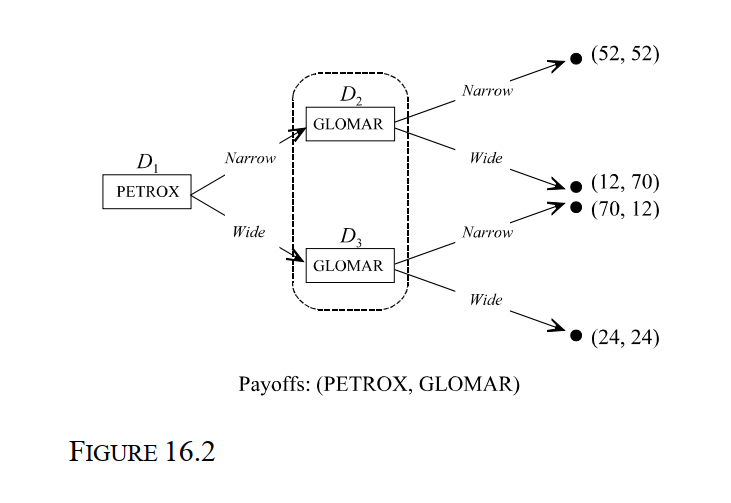 -Consider the static oil-drilling game depicted in Figure 16.2. The Nash equilibrium strategy profile for this game is:
-Consider the static oil-drilling game depicted in Figure 16.2. The Nash equilibrium strategy profile for this game is:
Free
(Multiple Choice)
4.8/5  (34)
(34)
Correct Answer:
C
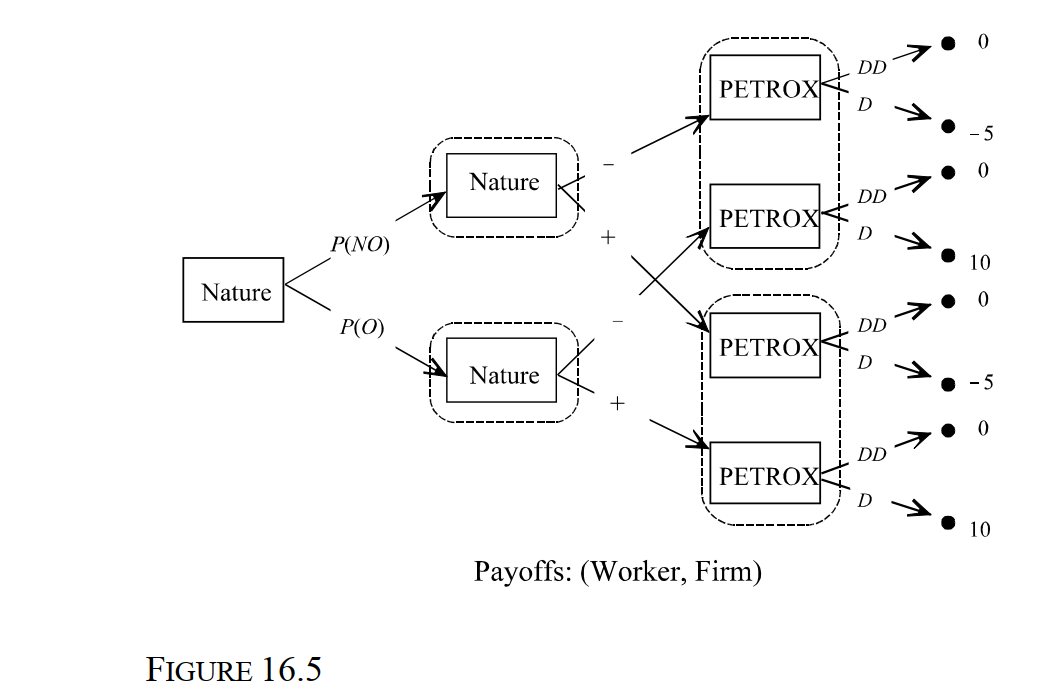 -Consider the Oil Drilling Game depicted in Figure 16.5. PETROX must decide whether to purchase a lease to drill for oil. Based on preliminary surveys, PETROX knows that there is an 80 percent chance that there is no oil (NO) and a 20 percent probability that oil is present (O). PETROX decides to conduct seismic surveys. The probability that the survey is negative when oil is present is P(!*O) = 0.5. The probability that there the survey is positive when no oil is present is P(+*NO) = 0.5. Payoffs are in millions of dollars. What is the probability that PETROX will strike oil when the seismic surveys indicate that oil is present?
-Consider the Oil Drilling Game depicted in Figure 16.5. PETROX must decide whether to purchase a lease to drill for oil. Based on preliminary surveys, PETROX knows that there is an 80 percent chance that there is no oil (NO) and a 20 percent probability that oil is present (O). PETROX decides to conduct seismic surveys. The probability that the survey is negative when oil is present is P(!*O) = 0.5. The probability that there the survey is positive when no oil is present is P(+*NO) = 0.5. Payoffs are in millions of dollars. What is the probability that PETROX will strike oil when the seismic surveys indicate that oil is present?
Free
(Multiple Choice)
5.0/5  (30)
(30)
Correct Answer:
B
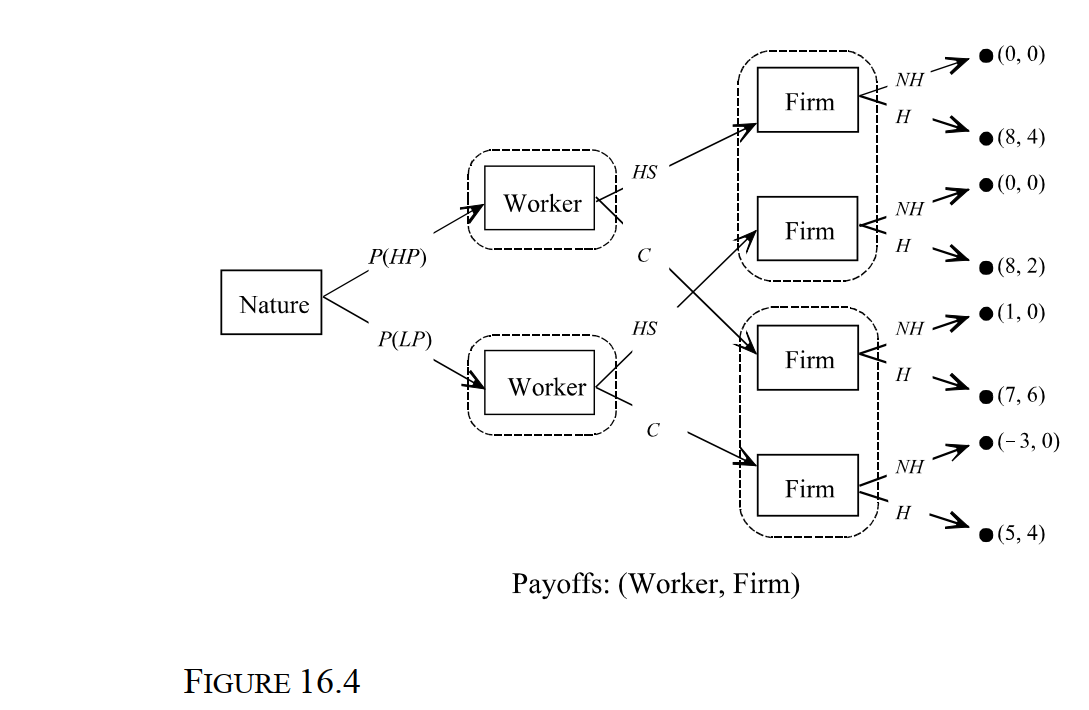 -Consider the Spence Education Game depicted in Figure 16.4. In the figure, all payoffs are in thousands of dollars per month. Suppose that 30 percent of all workers are low- productivity (LP) workers and 70 percent are high-productivity (HP) workers. Using pre- employment testing, the firm has determined that there is a 60 percent probability of hiring a high-school (HS) graduate who is also a high-productivity worker and a 75 percent probability of hiring a college (C) graduate who is a high-productivity worker. What is the probability that the firm will hire a low-productivity, high school graduate?
-Consider the Spence Education Game depicted in Figure 16.4. In the figure, all payoffs are in thousands of dollars per month. Suppose that 30 percent of all workers are low- productivity (LP) workers and 70 percent are high-productivity (HP) workers. Using pre- employment testing, the firm has determined that there is a 60 percent probability of hiring a high-school (HS) graduate who is also a high-productivity worker and a 75 percent probability of hiring a college (C) graduate who is a high-productivity worker. What is the probability that the firm will hire a low-productivity, high school graduate?
(Multiple Choice)
4.9/5  (39)
(39)
 -Consider the Oil Drilling Game depicted in Figure 16.5. PETROX must decide whether to purchase a lease to drill for oil. Based on preliminary surveys, PETROX knows that there is an 80 percent chance that there is no oil (NO) and a 20 percent probability that oil is present (O). PETROX decides to conduct seismic surveys. The probability that the survey is negative when oil is present is P(!*O) = 0.5. The probability that there the survey is positive when no oil is present is P(+*NO) = 0.5. Payoffs are in millions of dollars. What is PETROX's conditional expected payoff from drilling?
-Consider the Oil Drilling Game depicted in Figure 16.5. PETROX must decide whether to purchase a lease to drill for oil. Based on preliminary surveys, PETROX knows that there is an 80 percent chance that there is no oil (NO) and a 20 percent probability that oil is present (O). PETROX decides to conduct seismic surveys. The probability that the survey is negative when oil is present is P(!*O) = 0.5. The probability that there the survey is positive when no oil is present is P(+*NO) = 0.5. Payoffs are in millions of dollars. What is PETROX's conditional expected payoff from drilling?
(Multiple Choice)
4.8/5  (43)
(43)
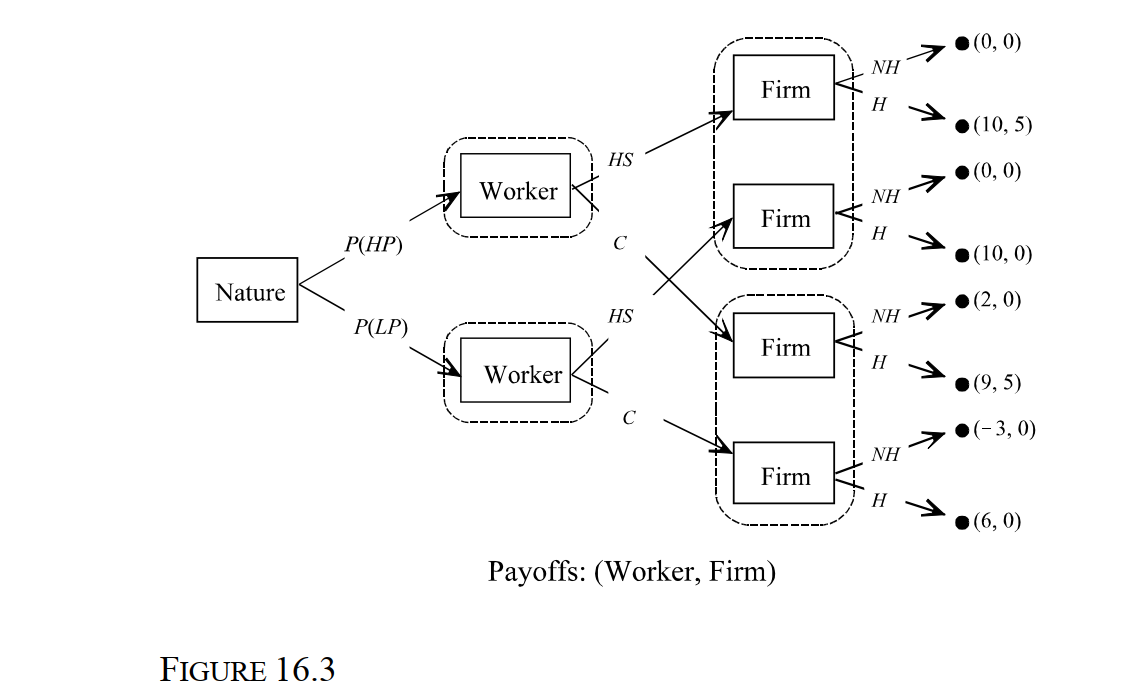 -Consider the Spence Education Game depicted in Figure 16.3. In the figure, all payoffs are in thousands of dollars per month. Suppose that 70 percent of all workers are low- productivity (LP) workers and 30 percent are high-productivity (HP) workers. Using pre- employment testing, the firm has determined that there is a 60 percent probability of hiring a high-school (HS) graduate who is also a high-productivity worker and a 75 percent probability of hiring a college (C) graduate who is a high-productivity worker. What is the firm's conditional expected payoff from hiring a college graduate?
-Consider the Spence Education Game depicted in Figure 16.3. In the figure, all payoffs are in thousands of dollars per month. Suppose that 70 percent of all workers are low- productivity (LP) workers and 30 percent are high-productivity (HP) workers. Using pre- employment testing, the firm has determined that there is a 60 percent probability of hiring a high-school (HS) graduate who is also a high-productivity worker and a 75 percent probability of hiring a college (C) graduate who is a high-productivity worker. What is the firm's conditional expected payoff from hiring a college graduate?
(Multiple Choice)
4.8/5  (33)
(33)
 -Consider the Spence Education Game depicted in Figure 16.4. In the figure, all payoffs are in thousands of dollars per month. Suppose that 30 percent of workers are low- productivity (LP) workers and 70 percent are high-productivity (HP) workers. Using pre- employment testing, the firm has determined that there is a 60 percent probability of hiring a high-school (HS) graduate who is also a high-productivity worker and a 75 percent probability of hiring a college (C) graduate who is a high-productivity worker. What is the firm's conditional expected payoff from hiring a high school graduate?
-Consider the Spence Education Game depicted in Figure 16.4. In the figure, all payoffs are in thousands of dollars per month. Suppose that 30 percent of workers are low- productivity (LP) workers and 70 percent are high-productivity (HP) workers. Using pre- employment testing, the firm has determined that there is a 60 percent probability of hiring a high-school (HS) graduate who is also a high-productivity worker and a 75 percent probability of hiring a college (C) graduate who is a high-productivity worker. What is the firm's conditional expected payoff from hiring a high school graduate?
(Multiple Choice)
4.9/5  (33)
(33)
 -Consider the Spence Education Game depicted in Figure 16.4. In the figure, all payoffs are in thousands of dollars per month. Suppose that 30 percent of workers are low- productivity (LP) workers and 70 percent are high-productivity (HP) workers. Using pre- employment testing, the firm has determined that there is a 60 percent probability of hiring a high-school (HS) graduate who is also a high-productivity worker and a 75 percent probability of hiring a college (C) graduate who is a high-productivity worker. What is the probability that the firm will hire a low-productivity worker who is a college graduate?
-Consider the Spence Education Game depicted in Figure 16.4. In the figure, all payoffs are in thousands of dollars per month. Suppose that 30 percent of workers are low- productivity (LP) workers and 70 percent are high-productivity (HP) workers. Using pre- employment testing, the firm has determined that there is a 60 percent probability of hiring a high-school (HS) graduate who is also a high-productivity worker and a 75 percent probability of hiring a college (C) graduate who is a high-productivity worker. What is the probability that the firm will hire a low-productivity worker who is a college graduate?
(Multiple Choice)
4.9/5  (37)
(37)
 -Consider the Spence Education Game depicted in Figure 16.4. In the figure, all payoffs are in thousands of dollars per month. Suppose there is a 30 percent of workers are low- productivity (LP) workers and 70 percent are high-productivity (HP) workers. Using pre- employment testing, the firm decides to adopt a separating strategy by assuming that only high-productivity workers go to college and that workers who have only graduated high school are low-productivity types. What is the firm's conditional expected payoff from hiring a college graduate?
-Consider the Spence Education Game depicted in Figure 16.4. In the figure, all payoffs are in thousands of dollars per month. Suppose there is a 30 percent of workers are low- productivity (LP) workers and 70 percent are high-productivity (HP) workers. Using pre- employment testing, the firm decides to adopt a separating strategy by assuming that only high-productivity workers go to college and that workers who have only graduated high school are low-productivity types. What is the firm's conditional expected payoff from hiring a college graduate?
(Multiple Choice)
4.8/5  (38)
(38)
 -Consider the Spence Education Game depicted in Figure 16.3. In the figure, all payoffs are in thousands of dollars per month. Suppose that 70 percent of all workers are low- productivity (LP) workers and 30 percent are high-productivity (HP) workers. Using pre- employment testing, the firm has determined that there is a 60 percent probability of hiring a high-school (HS) graduate who is also a high-productivity worker and a 75 percent probability of hiring a college (C) graduate who is a high-productivity worker. What is the probability that the firm will hire a low-productivity worker who is a high school graduate?
-Consider the Spence Education Game depicted in Figure 16.3. In the figure, all payoffs are in thousands of dollars per month. Suppose that 70 percent of all workers are low- productivity (LP) workers and 30 percent are high-productivity (HP) workers. Using pre- employment testing, the firm has determined that there is a 60 percent probability of hiring a high-school (HS) graduate who is also a high-productivity worker and a 75 percent probability of hiring a college (C) graduate who is a high-productivity worker. What is the probability that the firm will hire a low-productivity worker who is a high school graduate?
(Multiple Choice)
4.8/5  (30)
(30)
 -Consider the Oil Drilling Game depicted in Figure 16.5. PETROX must decide whether to purchase a lease to drill for oil. Based on preliminary surveys, PETROX knows that there is an 80 percent chance that there is no oil (NO) and a 20 percent probability that oil is present (O). PETROX decides to conduct seismic surveys. The probability that the survey is negative when oil is present is P(!*O) = 0.5. The probability that there the survey is positive when no oil is present is P(+*NO) = 0.5. Payoffs are in millions of dollars. What is the probability that PETROX will not strike oil when the seismic surveys indicate that oil is present?
-Consider the Oil Drilling Game depicted in Figure 16.5. PETROX must decide whether to purchase a lease to drill for oil. Based on preliminary surveys, PETROX knows that there is an 80 percent chance that there is no oil (NO) and a 20 percent probability that oil is present (O). PETROX decides to conduct seismic surveys. The probability that the survey is negative when oil is present is P(!*O) = 0.5. The probability that there the survey is positive when no oil is present is P(+*NO) = 0.5. Payoffs are in millions of dollars. What is the probability that PETROX will not strike oil when the seismic surveys indicate that oil is present?
(Multiple Choice)
4.8/5  (21)
(21)
 -Consider the static oil-drilling game depicted in Figure 16.2. The decision nodes D2 and D3 are collectively referred to as:
-Consider the static oil-drilling game depicted in Figure 16.2. The decision nodes D2 and D3 are collectively referred to as:
(Multiple Choice)
4.9/5  (39)
(39)
 -Consider the Spence Education Game depicted in Figure 16.3. In the figure, all payoffs are in thousands of dollars per month. Suppose that 70 percent of all workers are low- productivity (LP) workers and 30 percent are high-productivity (HP) workers. Using pre- employment testing, the firm has determined that there is a 60 percent probability of hiring a high-school (HS) graduate who is also a high-productivity worker and a 75 percent probability of hiring a college (C) graduate who is a high-productivity worker. What is the probability that the firm will hire a high-productivity worker who is a college graduate?
-Consider the Spence Education Game depicted in Figure 16.3. In the figure, all payoffs are in thousands of dollars per month. Suppose that 70 percent of all workers are low- productivity (LP) workers and 30 percent are high-productivity (HP) workers. Using pre- employment testing, the firm has determined that there is a 60 percent probability of hiring a high-school (HS) graduate who is also a high-productivity worker and a 75 percent probability of hiring a college (C) graduate who is a high-productivity worker. What is the probability that the firm will hire a high-productivity worker who is a college graduate?
(Multiple Choice)
4.9/5  (35)
(35)
 -Consider the Spence Education Game depicted in Figure 16.4. In the figure, all payoffs are in thousands of dollars per month. Suppose that 30 percent of all workers are low- productivity (LP) workers and 70 percent are high-productivity (HP) workers. Using pre- employment testing, the firm has determined that there is a 60 percent probability of hiring a high-school (HS) graduate who is also a high-productivity worker and a 75 percent probability of hiring a college (C) graduate who is a high-productivity worker. What is the probability that the firm will hire a high-productivity worker who is a high school graduate?
-Consider the Spence Education Game depicted in Figure 16.4. In the figure, all payoffs are in thousands of dollars per month. Suppose that 30 percent of all workers are low- productivity (LP) workers and 70 percent are high-productivity (HP) workers. Using pre- employment testing, the firm has determined that there is a 60 percent probability of hiring a high-school (HS) graduate who is also a high-productivity worker and a 75 percent probability of hiring a college (C) graduate who is a high-productivity worker. What is the probability that the firm will hire a high-productivity worker who is a high school graduate?
(Multiple Choice)
4.7/5  (30)
(30)
 -Consider the Spence Education Game depicted in Figure 16.3. In the figure, all payoffs are in thousands of dollars per month. Suppose that 70 percent of all workers are low- productivity (LP) workers and 30 percent are high-productivity (HP) workers. Using pre- employment testing, the firm has determined that there is a 60 percent probability of hiring a high-school (HS) graduate who is also a high-productivity worker and a 75 percent probability of hiring a college (C) graduate who is a high-productivity worker. What is the probability that the firm will hire a low-productivity worker who is a college graduate?
-Consider the Spence Education Game depicted in Figure 16.3. In the figure, all payoffs are in thousands of dollars per month. Suppose that 70 percent of all workers are low- productivity (LP) workers and 30 percent are high-productivity (HP) workers. Using pre- employment testing, the firm has determined that there is a 60 percent probability of hiring a high-school (HS) graduate who is also a high-productivity worker and a 75 percent probability of hiring a college (C) graduate who is a high-productivity worker. What is the probability that the firm will hire a low-productivity worker who is a college graduate?
(Multiple Choice)
4.8/5  (44)
(44)
 -Consider the Spence Education Game depicted in Figure 16.3. In the figure, all payoffs are in thousands of dollars per month. Suppose that 70 percent of all workers are low- productivity (LP) workers and 30 percent are high-productivity (HP) workers. Using pre- employment testing, the firm has determined that there is a 60 percent probability of hiring a high-school (HS) graduate who is also a high-productivity worker and a 75 percent probability of hiring a college (C) graduate who is a high-productivity worker. What is the optimal hiring strategy of a risk-neutral firm?
-Consider the Spence Education Game depicted in Figure 16.3. In the figure, all payoffs are in thousands of dollars per month. Suppose that 70 percent of all workers are low- productivity (LP) workers and 30 percent are high-productivity (HP) workers. Using pre- employment testing, the firm has determined that there is a 60 percent probability of hiring a high-school (HS) graduate who is also a high-productivity worker and a 75 percent probability of hiring a college (C) graduate who is a high-productivity worker. What is the optimal hiring strategy of a risk-neutral firm?
(Multiple Choice)
4.8/5  (44)
(44)
 -Consider the Spence Education Game depicted in Figure 16.3. In the figure, all payoffs are in thousands of dollars per month. Suppose that 70 percent of all workers are low- productivity (LP) workers and 30 percent are high-productivity (HP) workers. Using pre- employment testing, the firm decides to adopt a separating strategy by assuming that only high-productivity workers go to college and that workers who have only graduated high school are low-productivity types. What is the firm's conditional expected payoff from hiring a college graduate?
-Consider the Spence Education Game depicted in Figure 16.3. In the figure, all payoffs are in thousands of dollars per month. Suppose that 70 percent of all workers are low- productivity (LP) workers and 30 percent are high-productivity (HP) workers. Using pre- employment testing, the firm decides to adopt a separating strategy by assuming that only high-productivity workers go to college and that workers who have only graduated high school are low-productivity types. What is the firm's conditional expected payoff from hiring a college graduate?
(Multiple Choice)
4.7/5  (29)
(29)
Showing 1 - 20 of 34
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)