Exam 9: Markov Chains
Exam 1: Linear Equations and Graphs59 Questions
Exam 2: Functions and Graphs178 Questions
Exam 3: Mathematics of Finance57 Questions
Exam 4: Systems of Linear Equations; Matrices115 Questions
Exam 5: Linear Inequalities and Linear Programming26 Questions
Exam 6: Linear Programming: The Simplex Method58 Questions
Exam 7: Logic, Sets, and Counting51 Questions
Exam 8: Probability59 Questions
Exam 9: Markov Chains60 Questions
Exam 10: Data Description and Probability Distributions65 Questions
Exam 11: Games and Decisions52 Questions
Exam 12: Appendix A: Basic Algebra Review45 Questions
Exam 13: Appendix B: Special Topics20 Questions
Select questions type
The probability that an assembly line operation works correctly depends on whether it worked correctly the last time it was used. There is a 0.91 chance that the line will work correctly if it worked correctly the time before and a 0.68 chance that it will work correctly if it did not work correctly the time before. After setting up a transition matrix with this information, find the long-run probability that the line will work correctly.
Free
(Multiple Choice)
4.9/5  (36)
(36)
Correct Answer:
D
The transition matrix for a Markov process is:
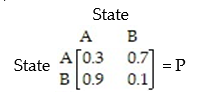 Find
Find 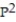 .
.
Free
(Multiple Choice)
4.8/5  (34)
(34)
Correct Answer:
A
Suppose that for a certain absorbing Markov chain the fundamental matrix is found to be 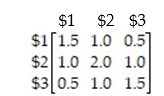 What is the expected number of times a person will have $3, given that he started with $2?
What is the expected number of times a person will have $3, given that he started with $2?
Free
(Multiple Choice)
4.9/5  (37)
(37)
Correct Answer:
A
Find the limiting matrix  corresponding to the transition matrix P =
corresponding to the transition matrix P = 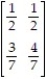 .Round to the nearest thousandths.
.Round to the nearest thousandths.
(Multiple Choice)
4.8/5  (35)
(35)
Find the limiting matrix  corresponding to the transition matrix P =
corresponding to the transition matrix P =  .Round to the nearest hundredths.
.Round to the nearest hundredths.
(Multiple Choice)
5.0/5  (32)
(32)
Find the limiting matrix  corresponding to the transition matrix P =
corresponding to the transition matrix P = 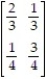 .Round to the nearest thousandths.
.Round to the nearest thousandths.
(Multiple Choice)
4.8/5  (35)
(35)
Find the fundamental matrix F for the absorbing Markov chain with the given matrix. Express your answer in fraction form. 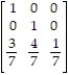
(Multiple Choice)
4.8/5  (29)
(29)
Given the transition matrix:
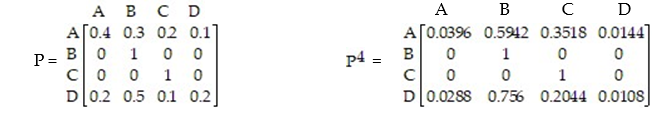 Find the probability of going from state D to state A in four trials.
Find the probability of going from state D to state A in four trials.
(Multiple Choice)
4.9/5  (37)
(37)
Laurinburg is experiencing a population movement out of the city to the suburbs. Currently 85% of the total population live in the city with the remaining 15% living in the suburbs. It has been shown that each year 7% of the city residents move to the suburbs, while only 1% of the suburb population move back to the city. Assuming population remains constant for both, what percent of the total will remain in the city after 5 years. Express your answer rounded to hundredths of a percent.
(Multiple Choice)
4.8/5  (44)
(44)
Find all absorbing states for the transition matrix, and indicate whether or not the matrix is that of an absorbing Markov chain. 
(Multiple Choice)
4.8/5  (37)
(37)
Find a standard form for the absorbing Markov chain with the transition matrix 
(Multiple Choice)
4.9/5  (33)
(33)
From statistics gathered over many seasons, it was determined that the probability a basketball player will make a basket after having made a basket on his previous attempt is .55, while the probability he will make a basket if he missed on his previous attempt is .48. In a current game a player has made 45% of his attempted shots. If the player shoots many more times in the game, what would be the overall percentage of baskets that he makes in this game?
(Multiple Choice)
4.9/5  (32)
(32)
The transition matrix for a Markov process is: 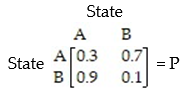 Find the second state matrix if the initial state is
Find the second state matrix if the initial state is 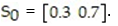
(Multiple Choice)
4.8/5  (37)
(37)
Find a standard form for the absorbing Markov chain with the transition matrix 
(Multiple Choice)
4.9/5  (37)
(37)
A red urn contains 4 red marbles, 2 blue marbles, and 4 green marbles. A blue urn contains 2 red marbles, 2 blue marbles, and 1 green marble. A green urn contains 3 green marbles. A marble is selected from an urn, the color is noted, and the marble is returned to the urn from which it was drawn. The next marble is drawn from the urn whose color is the same as the marble just drawn. Thus, this is a Markov process with three states: draw from the red urn, draw from the blue urn, or draw from the green urn.Write the transition matrix P.
(Multiple Choice)
4.8/5  (32)
(32)
Suppose that for a certain absorbing Markov chain the fundamental matrix is found to be  What is the expected number of times a person will have $3, given that she started with $1?
What is the expected number of times a person will have $3, given that she started with $1?
(Multiple Choice)
4.8/5  (32)
(32)
Showing 1 - 20 of 60
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)