Exam 9: Markov Chains
Exam 1: Linear Equations and Graphs59 Questions
Exam 2: Functions and Graphs178 Questions
Exam 3: Mathematics of Finance57 Questions
Exam 4: Systems of Linear Equations; Matrices115 Questions
Exam 5: Linear Inequalities and Linear Programming26 Questions
Exam 6: Linear Programming: The Simplex Method58 Questions
Exam 7: Logic, Sets, and Counting51 Questions
Exam 8: Probability59 Questions
Exam 9: Markov Chains60 Questions
Exam 10: Data Description and Probability Distributions65 Questions
Exam 11: Games and Decisions52 Questions
Exam 12: Appendix A: Basic Algebra Review45 Questions
Exam 13: Appendix B: Special Topics20 Questions
Select questions type
Find the stationary matrix for the transition matrix P =  Round the numbers in your answer to the nearest hundredth.
Round the numbers in your answer to the nearest hundredth.
(Multiple Choice)
4.8/5  (31)
(31)
According to data collected during one year in a large metropolitan community, 30% of commuters used public transportation to get to work, and this rose by 4% the following year. This is modeled by the transition matrix 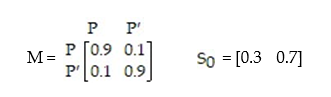 where P represents the percentage of people that use public transportation and
where P represents the percentage of people that use public transportation and  the percentage of people that do not.
What percentage of commuters in this community will use public transportation in the long run?
the percentage of people that do not.
What percentage of commuters in this community will use public transportation in the long run?
(Multiple Choice)
4.8/5  (45)
(45)
Fayetteville is experiencing a population movement out of the city to the suburbs. Currently 85% of the total population live in the city with the remaining 15% living in the suburbs. It has been shown that each year 7% of the city residents move to the suburbs, while only 1% of the suburb population move back to the city. Assuming population remains constant for both, what percent of the total will remain in the suburbs after 5 years. Express your answer rounded to hundredths of a percent.
(Multiple Choice)
4.9/5  (34)
(34)
Given the transition matrix:
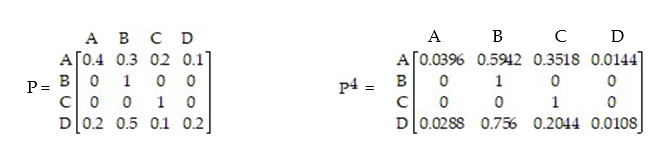 Find the probability of going from state C to state B in four trials.
Find the probability of going from state C to state B in four trials.
(Multiple Choice)
4.8/5  (30)
(30)
The probability that a car owner will become a car renter in five years is 0.03. The probability that a renter will become an owner in five years is 0.1. Suppose the proportions in the population are 64% owners (O), 35.5% renters (R) and .5% neither (N) with the following transition matrix. 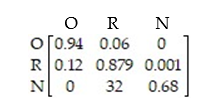
(Multiple Choice)
4.9/5  (38)
(38)
A trailer rental company has rental and return facilities at both a north and south location in a city. Assume a trailer must be returned to one or the other of these locations. If a trailer is rented at the north location, the probability that it will be returned there is .6; if a trailer is rented at the south location, the probability it will be returned there is .65. Assume the company rents all of its trailers each day and each trailer is rented (and returned) only once a day. If the company starts with 50% of the trailers at each location, what is the expected distribution (in percentages) the next day?
(Multiple Choice)
4.8/5  (39)
(39)
Find the stationary matrix for the transition matrix P =  Round the numbers in your answer to the nearest hundredth.
Round the numbers in your answer to the nearest hundredth.
(Multiple Choice)
4.8/5  (36)
(36)
A small town has only two dry cleaners, Fast and Speedy. Fast hopes to increase its market share by conducting an extensive advertising campaign. The initial market share for Fast was 40% and 60% for Speedy. Solve the problem:
-Find the probability that a customer using Fast initially will use Fast for his second batch of clothes. Use the following transition matrix.

(Multiple Choice)
4.9/5  (40)
(40)
Find all absorbing states for the transition matrix, and indicate whether or not the matrix is that of an absorbing Markov chain. 
(Multiple Choice)
4.8/5  (41)
(41)
Among patients who were improving on a certain day (in the critical care unit of a certain hospital), the following was determined to be true on the next day: 58% were still improving; 10% were stable; 7% were deteriorating; and 25% had been discharged. Among the patients who were stable on a certain day, the following was determined to be true on the next day: 34% were improving; 44% were still stable; 18% were deteriorating; 3% had been discharged; and 1% had died. Among the patients who were deteriorating on a certain day, the following was determined to be true on the next day: 13% were improving; 42% were stable; 41% were still deteriorating; none had been discharged; and 4% had died. What is the expected number of additional days that a patient, who is improving on that certain day, will spend in the critical care unit? Round your answer to the nearest hundredth.
(Multiple Choice)
4.8/5  (32)
(32)
Dublin is experiencing a population movement out of the city to the suburbs. Currently 85% of the total population live in the city with the remaining 15% living in the suburbs. It has been shown that each year 7% of the city residents move to the suburbs, while only 1% of the suburb population move back to the city. Assuming population remains constant for both, what percent of the total will remain in the city after 2 years. Express your answer rounded to hundredths of a percent.
(Multiple Choice)
4.8/5  (40)
(40)
Find a standard form for the absorbing Markov chain with the following transition matrix 
(Multiple Choice)
4.8/5  (40)
(40)
Rats are kept in a cage with two compartments (A and B). Rats in A move to B with probability 0.7. Rats in B move to A with probability 0.2. Find the long-term trend for rats in each compartment. Round numbers to the nearest thousandth.
(Multiple Choice)
4.8/5  (40)
(40)
Weather is classified as sunny or cloudy in a certain place. What are the long-term predictions for sunny and cloudy days? Round numbers to the nearest thousandths. 
(Multiple Choice)
4.9/5  (40)
(40)
According to data collected during one year in a large metropolitan community, 30% of commuters used public transportation to get to work, and this rose by 4% the following year. This is modeled by the transition matrix 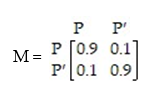 where P represents the percentage of people that use public transportation and
where P represents the percentage of people that use public transportation and 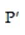 the percentage of people that do not. Let
the percentage of people that do not. Let 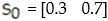 Find
Find 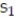 .
.
(Multiple Choice)
4.8/5  (36)
(36)
Showing 21 - 40 of 60
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)