Exam 11: Games and Decisions
Exam 1: Linear Equations and Graphs59 Questions
Exam 2: Functions and Graphs178 Questions
Exam 3: Mathematics of Finance57 Questions
Exam 4: Systems of Linear Equations; Matrices115 Questions
Exam 5: Linear Inequalities and Linear Programming26 Questions
Exam 6: Linear Programming: The Simplex Method58 Questions
Exam 7: Logic, Sets, and Counting51 Questions
Exam 8: Probability59 Questions
Exam 9: Markov Chains60 Questions
Exam 10: Data Description and Probability Distributions65 Questions
Exam 11: Games and Decisions52 Questions
Exam 12: Appendix A: Basic Algebra Review45 Questions
Exam 13: Appendix B: Special Topics20 Questions
Select questions type
Find the smallest integer k ≥ 0 such that adding k to each entry of the given matrix produces a matrix with all positive payoffs:
-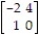
Free
(Multiple Choice)
4.7/5  (25)
(25)
Correct Answer:
D
Find the saddle values, if it exists, for the matrix game (include row and column location). 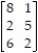
Free
(Multiple Choice)
4.9/5  (36)
(36)
Correct Answer:
D
In a two-finger Morra game, if player R matches player C, then R wins and if R and C don't match, then C wins. R will win $3 with one finger or two fingers, while C will win $1 with one finger and $5 with 2 fingers. The payoff matrix is 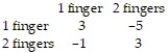 Find the optimal strategies
Find the optimal strategies  and
and 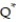 for R and C respectively, and the value v of the game.
for R and C respectively, and the value v of the game.
Free
(Multiple Choice)
4.9/5  (42)
(42)
Correct Answer:
D
A company has three different marketing strategies that produce different results depending upon whether inflation is above 6%, between 3% and 6% inclusive, or below 3% annually. The experts cannot predict inflation for the next year. The company has three plans of action and will implement these at varying percentages of its total operation. The payoff matrix for these three plans is given below, with values given in hundred thousands. What is the market strategy for the company that will yield the best expected value? 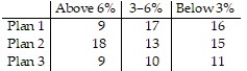
(Multiple Choice)
4.9/5  (34)
(34)
Use the simplex method to find the optimum strategy for players A and B and the value of the game for the payoff matrix:
-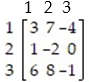
(Multiple Choice)
4.7/5  (30)
(30)
A person has hired an investment broker to buy stock. The broker has three different stock funds that are of interest, but each is sensitive to a certain economic indicator that is impossible to predict. The indicator will be positive, neutral, or negative. The table below shows the payoffs in thousands of dollars. Find the strategy that the broker should recommend to maximize the expected value of the investment. 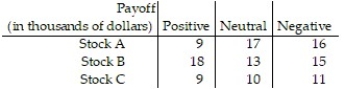
(Multiple Choice)
4.8/5  (38)
(38)
Find the expected value of the game matrix A =  if player 1 and player 2 decide on strategies
if player 1 and player 2 decide on strategies 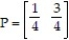 and Q =
and Q =  .
.
(Multiple Choice)
4.9/5  (34)
(34)
Determine which row(s) and column(s) of the game matrix are recessive.

(Multiple Choice)
4.8/5  (36)
(36)
Solve the matrix game using a geometric linear programming approach.
M = 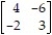
(Multiple Choice)
4.9/5  (41)
(41)
Find the saddle values, if it exists, for the matrix game (include row and column location). 
(Multiple Choice)
4.8/5  (35)
(35)
Suppose a matrix game has the following nonstrictly determined matrix:
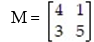 Set up (but do not solve), the two corresponding linear programming problem used to solve this matrix game.
Set up (but do not solve), the two corresponding linear programming problem used to solve this matrix game.
(Multiple Choice)
4.7/5  (29)
(29)
Two merchants in the same city plan on selling a new product. Each merchant has 3 strategies to enhance sales. The strategies chosen by each will determine the percentage of sales of the product each gets.
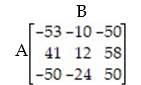
(Multiple Choice)
4.8/5  (25)
(25)
Two racquetball clubs are in competition in attracting new members. Advertising campaigns are being contemplated by both clubs which emphasize either beginning, intermediate, or advanced player tournaments among members. After careful research, the following results were found:
 Thus, if beginner tournaments are featured by both clubs, Club A expects to attract 25% of the new members and Club B expects to attract 75% of the new members, etc. Find the value of the game.
Thus, if beginner tournaments are featured by both clubs, Club A expects to attract 25% of the new members and Club B expects to attract 75% of the new members, etc. Find the value of the game.
(Multiple Choice)
4.9/5  (36)
(36)
Daisy and Gus write down one of the numbers 1, 4 , or 7. If the sum of the numbers is even Daisy pays Gus that number of dimes. If the sum of the numbers is odd, Gus pays Daisy that number of dimes. Write Daisy's game matrix that corresponds to this situation.
(Multiple Choice)
4.9/5  (42)
(42)
The matrix for a strictly determined matrix game is given below. Determine if the game is fair or not fair. 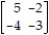
(Multiple Choice)
4.8/5  (41)
(41)
Use the simplex method to find the optimum strategy for players A and B and the value of the game for the payoff matrix:
-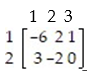
(Multiple Choice)
4.9/5  (37)
(37)
QMC decided to put its new product on the market with ads in a trade magazine and a booth at a trade show. It found out that its major competitor ZMC also had decided to advertise the same way for its new product. The payoff matrix shows the increased sales for QMC, as well as decreased sales for ZMC. What is the optimum strategy for QMC and the value of the game? 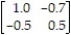
(Multiple Choice)
4.7/5  (37)
(37)
Delete recessive rows and columns from the following matrix game:

(Multiple Choice)
4.8/5  (26)
(26)
Showing 1 - 20 of 52
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)