Exam 7: Logic, Sets, and Counting
Exam 1: Linear Equations and Graphs59 Questions
Exam 2: Functions and Graphs178 Questions
Exam 3: Mathematics of Finance57 Questions
Exam 4: Systems of Linear Equations; Matrices115 Questions
Exam 5: Linear Inequalities and Linear Programming26 Questions
Exam 6: Linear Programming: The Simplex Method58 Questions
Exam 7: Logic, Sets, and Counting51 Questions
Exam 8: Probability59 Questions
Exam 9: Markov Chains60 Questions
Exam 10: Data Description and Probability Distributions65 Questions
Exam 11: Games and Decisions52 Questions
Exam 12: Appendix A: Basic Algebra Review45 Questions
Exam 13: Appendix B: Special Topics20 Questions
Select questions type
Construct a truth table for the proposition:
-p ~q
Free
(Multiple Choice)
4.8/5  (31)
(31)
Correct Answer:
C
Use the addition principle for counting to solve the problem:
-If n(A) = 20, n(A B) = 58, and n(A B) = 16, find n(B).
Free
(Multiple Choice)
4.9/5  (38)
(38)
Correct Answer:
B
Use the addition principle for counting to solve the problem:
-If n(A) = 5, n(B) = 11 and n(A B) = 3, what is n(A B)?
Free
(Multiple Choice)
4.8/5  (32)
(32)
Correct Answer:
C
Tell whether the statement is true or false:
-7 0 {14, 21, 28, 35, 42}
(True/False)
4.7/5  (35)
(35)
Use the addition principle for counting to solve the problem:
-If n(A) = 40, n(B) = 117 and n(A B) = 137, what is n(A B)?
(Multiple Choice)
4.9/5  (45)
(45)
Use a Venn Diagram and the given information to determine the number of elements in the indicated region:
-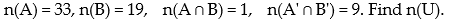
(Multiple Choice)
4.8/5  (37)
(37)
Use a Venn Diagram and the given information to determine the number of elements in the indicated region:
-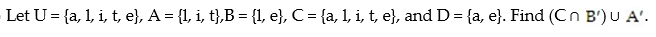
(Short Answer)
4.7/5  (42)
(42)
Construct a truth table to decide if the two statements are equivalent:
-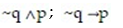
(True/False)
4.8/5  (29)
(29)
Mrs. Bollo's second grade class of thirty students conducted a pet ownership survey. Results of the survey indicate that 8 students own a cat, 15 students own a dog, and 5 students own both a cat and a dog. How many of the students surveyed own no dogs?
(Multiple Choice)
4.8/5  (32)
(32)
Let A = {6, 4, 1, {3, 0, 8}, {9}}. Determine whether the statement is true or false
-{3, 0, 8} A
(True/False)
4.9/5  (36)
(36)
Construct a truth table to decide if the two statements are equivalent:
-~p ~q; ~(p 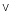 q)
q)
(True/False)
4.9/5  (39)
(39)
Let A = {1, 3, 5, 7}; B = {5, 6, 7, 8}; C = {5, 8}; andU= {1,2,3,4,5,6,7,8} Determine whether the given statement is true or false.
-C D
(True/False)
4.8/5  (32)
(32)
Determine whether the given set is finite or infinite. Consider the set N of positive integers to be the universal set, and let
A = {n ∈ N| n > 50}
B = {n ∈ N| n < 250}
O = {n ∈ N| n is odd}
E = {n ∈ N| n is even}
-A'
(Multiple Choice)
4.9/5  (34)
(34)
Let A = {1, 3, 5, 7}; B = {5, 6, 7, 8}; C = {5, 8}; andU= {1,2,3,4,5,6,7,8} Determine whether the given statement is true or false.
-U A
(True/False)
4.9/5  (29)
(29)
Construct a truth table for the proposition and determine whether it is a contingency, a tautology, or a contradiction: ~p ∨ q.
(Short Answer)
4.7/5  (30)
(30)
Use the Venn diagram below to find the number of elements in the region.
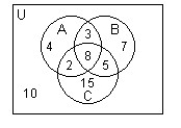 -n(A C)
-n(A C)
(Multiple Choice)
4.8/5  (40)
(40)
Showing 1 - 20 of 51
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)