Exam 2: Functions and Graphs
Exam 1: Linear Equations and Graphs59 Questions
Exam 2: Functions and Graphs178 Questions
Exam 3: Mathematics of Finance57 Questions
Exam 4: Systems of Linear Equations; Matrices115 Questions
Exam 5: Linear Inequalities and Linear Programming26 Questions
Exam 6: Linear Programming: The Simplex Method58 Questions
Exam 7: Logic, Sets, and Counting51 Questions
Exam 8: Probability59 Questions
Exam 9: Markov Chains60 Questions
Exam 10: Data Description and Probability Distributions65 Questions
Exam 11: Games and Decisions52 Questions
Exam 12: Appendix A: Basic Algebra Review45 Questions
Exam 13: Appendix B: Special Topics20 Questions
Select questions type
Graph by converting to exponential form first:
-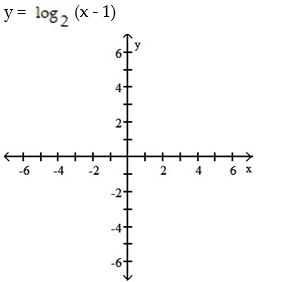
Free
(Multiple Choice)
4.8/5  (34)
(34)
Correct Answer:
A
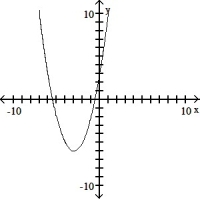
The graph that follows is the graph of a polynomial function. (i) What is the minimum degree of a polynomial function that could have the graph? (ii) Is the leading coefficient of the polynomial negative or positive?
-
Free
(Multiple Choice)
4.8/5  (37)
(37)
Correct Answer:
C
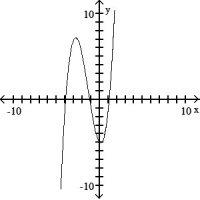
The graph that follows is the graph of a polynomial function. (i) What is the minimum degree of a polynomial function that could have the graph? (ii) Is the leading coefficient of the polynomial negative or positive?
-
(Multiple Choice)
4.8/5  (30)
(30)
Use a calculator to evaluate the expression. Round the result to five decimal places:
-log (-10.25)
(Multiple Choice)
4.9/5  (33)
(33)
Financial analysts in a company that manufactures ovens arrived at the following daily cost equation for manufacturing x ovens per day: C(x) = 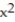 + 4x + 1800. The average cost per unit at a production level of x ovens per day is
+ 4x + 1800. The average cost per unit at a production level of x ovens per day is  (x) = C(x)/x. (i) Find the rational function
(x) = C(x)/x. (i) Find the rational function  . (ii) Sketch a graph of
. (ii) Sketch a graph of  (x) for 10 x 125. (iii) For what daily production level (to the nearest integer) is the average cost per unit at a minimum, and what is the minimum average cost per oven (to the nearest cent)? HINT: Refer to the sketch in part (ii) and evaluate
(x) for 10 x 125. (iii) For what daily production level (to the nearest integer) is the average cost per unit at a minimum, and what is the minimum average cost per oven (to the nearest cent)? HINT: Refer to the sketch in part (ii) and evaluate  (x) at appropriate integer values until a minimum value is found.
(x) at appropriate integer values until a minimum value is found. 
(Multiple Choice)
4.9/5  (35)
(35)
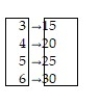
Determine whether the relation represents a function. If it is a function, state the domain and range.
-
(Multiple Choice)
4.9/5  (31)
(31)
Find the vertex form for the quadratic function. Then find each of the following:
(A) Intercepts
(B) Vertex
(C) Maximum or minimum
(D) Range
-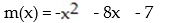
(Multiple Choice)
4.7/5  (30)
(30)
How can the graph of f(x) = - 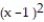 6 be obtained from the graph of y =
6 be obtained from the graph of y = 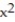 ?
?
(Multiple Choice)
4.8/5  (38)
(38)
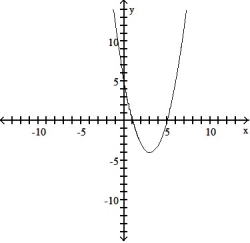
Write an equation for the lowest-degree polynomial function with the graph and intercepts shown in the figure:
-
(Multiple Choice)
4.7/5  (35)
(35)
Assume that a person's critical weight W, defined as the weight above which the risk of death rises dramatically, is given by W(h) = 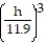 , where W is in pounds and h is the person's height in inches.Find the tcritical weight for a person who is 6 ft 11 in. tall. Round to the nearest tenth.
, where W is in pounds and h is the person's height in inches.Find the tcritical weight for a person who is 6 ft 11 in. tall. Round to the nearest tenth.
(Multiple Choice)
4.8/5  (34)
(34)
Find the range of the given function. Express your answer in interval notation:
-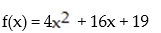
(Multiple Choice)
4.9/5  (24)
(24)
For the rational function below (i) Find the intercepts for the graph; (ii) Determine the domain; (iii) Find any vertical or horizontal asymptotes for the graph; (iv) Sketch any asymptotes as dashed lines. Then sketch the graph of y = f(x).
-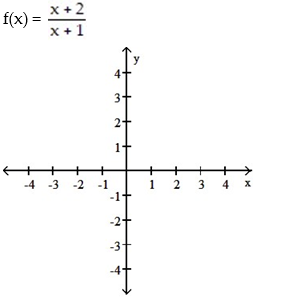
(Multiple Choice)
4.7/5  (32)
(32)
Determine whether the function is linear, constant, or neither:
-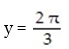
(Multiple Choice)
4.8/5  (44)
(44)
Showing 1 - 20 of 178
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)