Exam 7: Logic, Sets, and Counting
Exam 1: Linear Equations and Graphs59 Questions
Exam 2: Functions and Graphs178 Questions
Exam 3: Mathematics of Finance57 Questions
Exam 4: Systems of Linear Equations; Matrices115 Questions
Exam 5: Linear Inequalities and Linear Programming26 Questions
Exam 6: Linear Programming: The Simplex Method58 Questions
Exam 7: Logic, Sets, and Counting51 Questions
Exam 8: Probability59 Questions
Exam 9: Markov Chains60 Questions
Exam 10: Data Description and Probability Distributions65 Questions
Exam 11: Games and Decisions52 Questions
Exam 12: Appendix A: Basic Algebra Review45 Questions
Exam 13: Appendix B: Special Topics20 Questions
Select questions type
Determine whether the given set is finite or infinite. Consider the set N of positive integers to be the universal set, and let
A = {n ∈ N| n > 50}
B = {n ∈ N| n < 250}
O = {n ∈ N| n is odd}
E = {n ∈ N| n is even}
-B E
(Multiple Choice)
4.8/5  (28)
(28)
Use a Venn Diagram and the given information to determine the number of elements in the indicated region:
-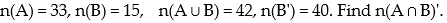
(Multiple Choice)
4.8/5  (41)
(41)
Tell whether the statement is true or false:
-3 {6, 9, 12, 15, 18}
(True/False)
4.9/5  (44)
(44)
One of the following is false; indicate by letter which one:
(Multiple Choice)
4.8/5  (38)
(38)
Construct a truth table to decide if the two statements are equivalent:
-~(~q); q
(True/False)
4.7/5  (30)
(30)
Let A = {1, 3, 5, 7}; B = {5, 6, 7, 8}; C = {5, 8}; andU= {1,2,3,4,5,6,7,8} Determine whether the given statement is true or false.
-A A
(True/False)
4.8/5  (36)
(36)
Let A = {6, 4, 1, {3, 0, 8}, {9}}. Determine whether the statement is true or false
-{9} A
(True/False)
4.9/5  (37)
(37)
Let A = {1, 3, 5, 7}; B = {5, 6, 7, 8}; C = {5, 8}; andU= {1,2,3,4,5,6,7,8} Determine whether the given statement is true or false.
-{5} D
(True/False)
4.8/5  (34)
(34)
Construct a truth table to decide if the two statements are equivalent:
-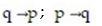
(True/False)
4.8/5  (36)
(36)
A local television station sends out questionnaires to determine if viewers would rather see a documentary, an interview show, or reruns of a game show. There were 300 responses with the following results:
90 were interested in an interview show and a documentary, but not reruns.
12 were interested in an interview show and reruns but not a documentary
42 were interested in reruns but not an interview show.
72 were interested in an interview show but not a documentary.
30 were interested in a documentary and reruns.
18 were interested in an interview show and reruns.
24 were interested in none of the three.
How many are interested in exactly one kind of show?
(Multiple Choice)
4.8/5  (33)
(33)
Construct a truth table to decide if the two statements are equivalent:
-~p 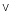 ~q; ~(p q)
~q; ~(p q)
(True/False)
4.8/5  (27)
(27)
Use the Venn diagram below to find the number of elements in the region.
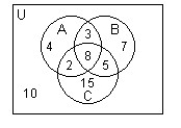 -n((A B) C)
-n((A B) C)
(Multiple Choice)
4.9/5  (44)
(44)
Use the Venn diagram below to find the number of elements in the region.
 -
-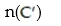
(Multiple Choice)
4.9/5  (37)
(37)
Showing 21 - 40 of 51
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)