Exam 6: Applications of Integration
Exam 1: Functions226 Questions
Exam 2: Limits224 Questions
Exam 3: Derivatives367 Questions
Exam 4: Applications of the Derivative228 Questions
Exam 5: Integration166 Questions
Exam 6: Applications of Integration211 Questions
Exam 7: Logarithmic, Exponential, and Hyperbolic Functions85 Questions
Exam 8: Integration Techniques287 Questions
Exam 9: Differential Equations76 Questions
Exam 10: Sequences and Infinite Series173 Questions
Exam 11: Power Series103 Questions
Exam 12: Parametric and Polar Curves169 Questions
Exam 13: Vectors and the Geometry of Space131 Questions
Exam 14: Vector-Valued Functions83 Questions
Exam 15: Functions of Several Variables229 Questions
Exam 16: Multiple Integration299 Questions
Exam 17: Vector Calculus173 Questions
Select questions type
Use the shell method to find the volume of the solid generated by revolving the shaded region about the indicated axis.
-About the y-axis
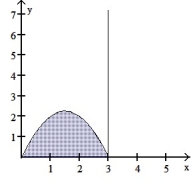
Free
(Multiple Choice)
4.8/5  (37)
(37)
Correct Answer:
B
Find the volume of the solid generated by revolving the region bounded by the given lines and curves about the 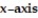 -y = 8x, y = 8, x = 0
-y = 8x, y = 8, x = 0
Free
(Multiple Choice)
4.8/5  (39)
(39)
Correct Answer:
A
Find the volume of the solid generated by revolving the region about the y-axis.
-The region enclosed by the triangle with vertices ( 1, 0), ( 1, 2), ( 3, 2)
Free
(Multiple Choice)
4.8/5  (39)
(39)
Correct Answer:
B
Solve the problem.
-A 25-kg mass is attached to a spring that hangs vertically and is stretched 1 m from the equilibrium position of the spring. Assume a linear spring with F(x) = kx. How much work is required to stretch the spring and lower the mass 1.5 m? Round to four decimal places when appropriate.
(Multiple Choice)
4.8/5  (33)
(33)
Find the volume of the solid generated by revolving the region bounded by the given lines and curves about the  -y = x, y = 0, x = 3, x = 5
-y = x, y = 0, x = 3, x = 5
(Multiple Choice)
4.8/5  (43)
(43)
Let R be the region bounded by the given curves. Find the volume of the solid generated when R is revolved about the given line.
-y = 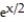 + 1, y = 1, x = 0, and x = 2; about y = 1
+ 1, y = 1, x = 0, and x = 2; about y = 1
(Multiple Choice)
4.9/5  (42)
(42)
Find the volume of the solid generated by revolving the shaded region about the given axis.
-About the y-axis 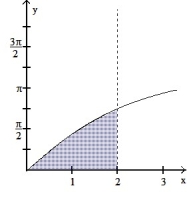

(Multiple Choice)
4.8/5  (35)
(35)
Find the volume of the solid generated by revolving the region about the given axis. Use the shell or washer method.
-The region bounded by y = 3x - 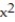 and y = x about the line x = 2
and y = x about the line x = 2
(Multiple Choice)
4.8/5  (32)
(32)
Find the volume of the described solid.
-The solid lies between planes perpendicular to the x-axis at  and
and 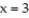 . The cross sections perpendicular to the x-axis between these planes are squares whose bases run from the semicircle
. The cross sections perpendicular to the x-axis between these planes are squares whose bases run from the semicircle 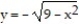 to the semicircle
to the semicircle 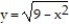 .
.
(Multiple Choice)
4.8/5  (30)
(30)
Use the shell method to find the volume of the solid generated by revolving the region bounded by the given curves and lines about the y-axis.
-y =  , y = 0, x = 2, x = 4
, y = 0, x = 2, x = 4
(Multiple Choice)
4.9/5  (31)
(31)
Solve the problem.
-A 50-m-long chain hangs vertically from a cylinder attached to a winch. Assume there is no friction in the system and that the chain has a density of 10 kg/m. How much work is required to wind the chain onto the cylinder if a 50-kg block is attached to the end of the chain?
(Multiple Choice)
4.8/5  (37)
(37)
Use the shell method to find the volume of the solid generated by revolving the region bounded by the given curves and lines about the y-axis.
-y = 32 - 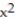 , y =
, y = 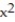 , x = 0
, x = 0
(Multiple Choice)
4.9/5  (25)
(25)
Find the volume of the described solid.
-The solid lies between planes perpendicular to the x-axis at 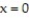 and
and 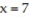 . The cross sections perpendicular to the x-axis between these planes are squares whose bases run from the parabola
. The cross sections perpendicular to the x-axis between these planes are squares whose bases run from the parabola 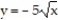 to the parabola
to the parabola 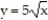 .
.
(Multiple Choice)
5.0/5  (40)
(40)
Use the shell method to find the volume of the solid generated by revolving the shaded region about the indicated axis.
-About the y-axis x = 2
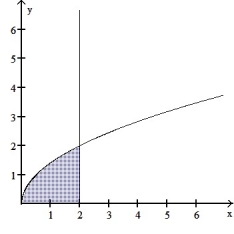

(Multiple Choice)
5.0/5  (32)
(32)
Solve the problem.
-A cylinder with height 9 m and radius 3 m is filled with water and must be emptied through an outlet pipe 3 m above the top of the cylinder. Compute the work required to empty the water in the top half of the tank. Then compute the work required to empty the (equal amount of) water in the lower half of the tank. Round to two decimal places when appropriate.
(Multiple Choice)
5.0/5  (39)
(39)
Use the shell method to find the volume of the solid generated by revolving the region bounded by the given curves and lines about the x-axis.
-x = 4y - 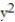 , x = 0
, x = 0
(Multiple Choice)
4.7/5  (40)
(40)
Find the volume of the solid generated by revolving the shaded region about the given axis.
-About the y-axis 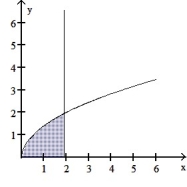

(Multiple Choice)
4.8/5  (37)
(37)
Find the area enclosed by the given curves.
-Find the area of the region between the curve y = 2x/(1 + 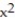 ) and the interval
) and the interval 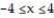 of the x-axis.
of the x-axis.
(Multiple Choice)
4.9/5  (42)
(42)
Solve the problem.
-A 25-kg mass is attached to a spring that hangs vertically and is stretched 3 m from the equilibrium position of the spring. Assume a linear spring with F(x) = kx. How much work is required to compress the spring and lift the mass 1.5 m? Round to four decimal places when appropriate.
(Multiple Choice)
4.8/5  (45)
(45)
Showing 1 - 20 of 211
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)