Exam 10: Inverse, Exponential, and Logarithmic Functions
Exam 1: Review of the Real Number System431 Questions
Exam 2: Linear Equations, Inequalities, and Applications338 Questions
Exam 3: Linear Equations, Graphs, and Functions347 Questions
Exam 4: Systems of Linear Equations166 Questions
Exam 5: Exponents, Polynomials, and Polynomial Functions327 Questions
Exam 6: Factoring180 Questions
Exam 7: Rational Expressions and Functions233 Questions
Exam 8: Roots, Radicals, and Root Functions358 Questions
Exam 9: Quadratic Equations, Inequalities, and Functions339 Questions
Exam 10: Inverse, Exponential, and Logarithmic Functions292 Questions
Exam 11: Nonlinear Functions, Conic Sections, and Nonlinear Systems233 Questions
Exam 12: Further Topics in Algebra190 Questions
Exam 13: Appendices29 Questions
Select questions type
When asked to describe logarithms in one simple sentence, the teacher said, "Logarithms are exponents". What is meant by this sentence?
(Short Answer)
4.8/5  (34)
(34)
The sales of a new product (in items per month) can be approximated by , where represents the number of months after the item first becomes available. Find the number of items sold per month 33 months after the item first becomes available.
(Multiple Choice)
4.9/5  (32)
(32)
Find the logarithm. Give an approximation to four decimal places
-
(Multiple Choice)
4.8/5  (34)
(34)
If , what two points on the graph of can be found with no computation?
(Short Answer)
4.9/5  (24)
(24)
The function can be used to estimate the number of years after 1980 required for a certain country's population to reach million people. In what year will the country's population reach 14 million?
(Multiple Choice)
4.9/5  (27)
(27)
Rewrite the given expression as a single logarithm. Assume that all variables are defined in such a way that variable expressions are positive and bases are positive numbers not equal to 1 .
-
(Multiple Choice)
4.9/5  (35)
(35)
Use the horizontal line test to determine if the function is one-to-one.
-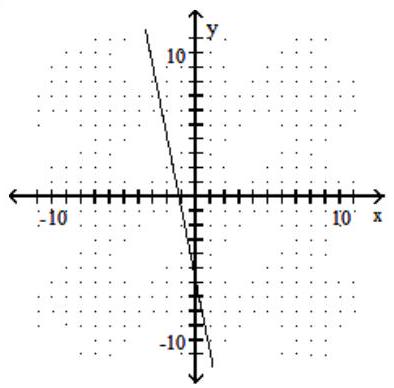
(True/False)
4.9/5  (39)
(39)
Find the logarithm. Give an approximation to four decimal places
-
(Multiple Choice)
4.9/5  (38)
(38)
Rewrite the given expression as a single logarithm. Assume that all variables are defined in such a way that variable expressions are positive and bases are positive numbers not equal to 1 .
-
(Multiple Choice)
4.8/5  (37)
(37)
Solve the equation. Give the solution to three decimal places.
-
(Multiple Choice)
4.8/5  (33)
(33)
Solve the equation. Give the exact solution or solutions.
-
(Multiple Choice)
4.8/5  (41)
(41)
Graph the given function as a solid line (or curve) and its inverse as a dashed line (or curve) on the same set of axes.
-
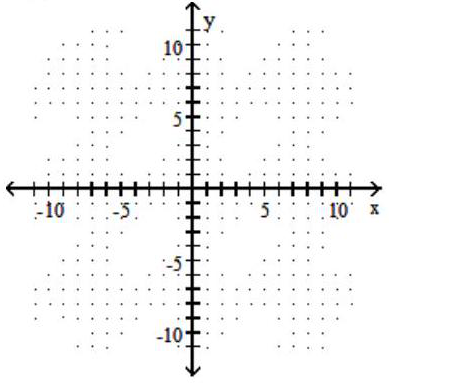
(Multiple Choice)
4.8/5  (34)
(34)
Solve the problem. Round your answer to the nearest tenth, when appropriate. Use the formula , as needed.
-Find if the .
(Multiple Choice)
4.9/5  (32)
(32)
Use properties of logarithms to write each expression as a sum or difference of logarithms. Assume that variables represent positive real numbers.
-
(Multiple Choice)
4.8/5  (35)
(35)
Showing 261 - 280 of 292
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)