Exam 10: Inverse, Exponential, and Logarithmic Functions
Exam 1: Review of the Real Number System431 Questions
Exam 2: Linear Equations, Inequalities, and Applications338 Questions
Exam 3: Linear Equations, Graphs, and Functions347 Questions
Exam 4: Systems of Linear Equations166 Questions
Exam 5: Exponents, Polynomials, and Polynomial Functions327 Questions
Exam 6: Factoring180 Questions
Exam 7: Rational Expressions and Functions233 Questions
Exam 8: Roots, Radicals, and Root Functions358 Questions
Exam 9: Quadratic Equations, Inequalities, and Functions339 Questions
Exam 10: Inverse, Exponential, and Logarithmic Functions292 Questions
Exam 11: Nonlinear Functions, Conic Sections, and Nonlinear Systems233 Questions
Exam 12: Further Topics in Algebra190 Questions
Exam 13: Appendices29 Questions
Select questions type
Rewrite the given expression as a single logarithm. Assume that all variables are defined in such a way that variable expressions are positive and bases are positive numbers not equal to 1 .
-
(Multiple Choice)
4.7/5  (33)
(33)
If the following defines a one-to-one function, find its inverse. If not, write "Not one-to-one."
-
(Multiple Choice)
4.8/5  (27)
(27)
If the following defines a one-to-one function, find its inverse. If not, write "Not one-to-one."
-
(Multiple Choice)
4.9/5  (31)
(31)
Solve the equation. Give the solution to three decimal places.
-
(Multiple Choice)
4.8/5  (36)
(36)
The table below gives the actual values of the population of a small island in the Pacific Ocean. The population is modeled by the equation , where represents the population of the island in 1990.
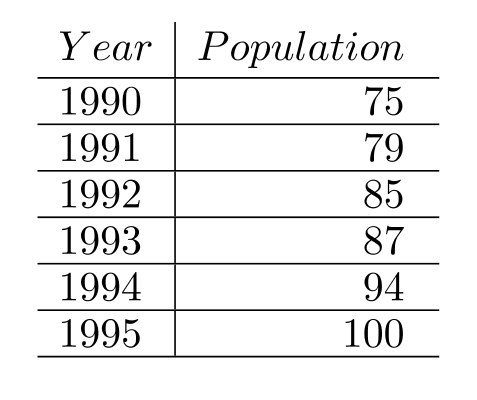
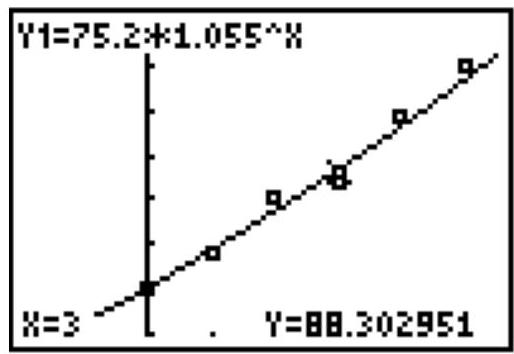 For the point displayed in the calculator screen above, how does the model compare to the actual?
For the point displayed in the calculator screen above, how does the model compare to the actual?
(Multiple Choice)
4.9/5  (35)
(35)
Find the logarithm. Give an approximation to four decimal places.
-
(Multiple Choice)
4.9/5  (32)
(32)
Find the logarithm. Give an approximation to four decimal places
-
(Multiple Choice)
4.8/5  (33)
(33)
The decibel level of a sound is related to its intensity by . If is , then what is the intensity of a noise measured at 78 decibels? Express your answer in scientific notation, rounding to three significant digits, if necessary.
(Multiple Choice)
4.8/5  (33)
(33)
If the following defines a one-to-one function, find its inverse. If not, write "Not one-to-one."
-
(Multiple Choice)
4.9/5  (30)
(30)
Determine whether or not the function is one-to-one.
-The function that pairs the temperature in degrees Fahrenheit of a cup of coffee with its temperature in degrees Celsius.
(True/False)
4.7/5  (27)
(27)
Find the logarithm. Give an approximation to four decimal places
-
(Multiple Choice)
4.8/5  (43)
(43)
Showing 161 - 180 of 292
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)