Exam 10: Inverse, Exponential, and Logarithmic Functions
Exam 1: Review of the Real Number System431 Questions
Exam 2: Linear Equations, Inequalities, and Applications338 Questions
Exam 3: Linear Equations, Graphs, and Functions347 Questions
Exam 4: Systems of Linear Equations166 Questions
Exam 5: Exponents, Polynomials, and Polynomial Functions327 Questions
Exam 6: Factoring180 Questions
Exam 7: Rational Expressions and Functions233 Questions
Exam 8: Roots, Radicals, and Root Functions358 Questions
Exam 9: Quadratic Equations, Inequalities, and Functions339 Questions
Exam 10: Inverse, Exponential, and Logarithmic Functions292 Questions
Exam 11: Nonlinear Functions, Conic Sections, and Nonlinear Systems233 Questions
Exam 12: Further Topics in Algebra190 Questions
Exam 13: Appendices29 Questions
Select questions type
Graph the given function as a solid line (or curve) and its inverse as a dashed line (or curve) on the same set of axes.
-
(Multiple Choice)
4.7/5  (38)
(38)
The screen shows a table of values for the function defined by .
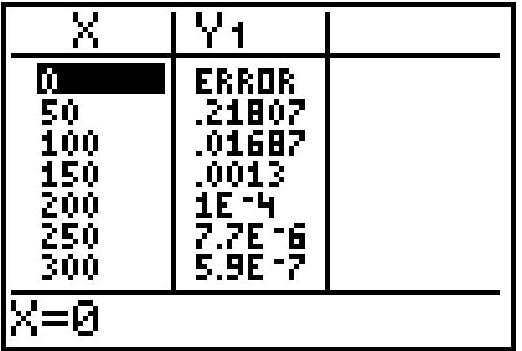 Why is there an error message for ?
Why is there an error message for ?
(Multiple Choice)
4.8/5  (26)
(26)
Find the amount of money in an account after 3 years if is deposited at annual interest compounded semiannually.
(Multiple Choice)
4.8/5  (48)
(48)
Why is e used as a base for exponential and logarithmic functions?
(Short Answer)
4.8/5  (36)
(36)
Use a calculator and the change-of-base formula to find the logarithm to four decimal places.
-
(Multiple Choice)
4.7/5  (30)
(30)
Why is finding the value of like answering the question "What is the name of the girl whose name is Jane?"
(Essay)
4.7/5  (33)
(33)
When solving a logarithmic equation, why must you always check that each solution works in the original equation?
(Short Answer)
4.7/5  (31)
(31)
Solve the equation. Use natural logarithms. When appropriate, give solutions to three decimal places unless otherwise indicated.
-
(Multiple Choice)
4.8/5  (34)
(34)
Using the exponential key of a calculator to find an approximation to the nearest thousandth.
-2.5973 .8
(Multiple Choice)
4.9/5  (33)
(33)
Find the logarithm. Give an approximation to four decimal places
-
(Multiple Choice)
4.8/5  (36)
(36)
Solve, giving the correct solution to four decimal places.
-
(Multiple Choice)
4.8/5  (37)
(37)
Is it possible to solve the equation by taking the natural logarithm of 4 , the common logarithm of 7 , and finding the quotient ? Explain.
(Essay)
4.7/5  (41)
(41)
Use a calculator and the change-of-base formula to find the logarithm to four decimal places.
-
(Multiple Choice)
4.8/5  (29)
(29)
Showing 141 - 160 of 292
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)