Exam 10: Inverse, Exponential, and Logarithmic Functions
Exam 1: Review of the Real Number System431 Questions
Exam 2: Linear Equations, Inequalities, and Applications338 Questions
Exam 3: Linear Equations, Graphs, and Functions347 Questions
Exam 4: Systems of Linear Equations166 Questions
Exam 5: Exponents, Polynomials, and Polynomial Functions327 Questions
Exam 6: Factoring180 Questions
Exam 7: Rational Expressions and Functions233 Questions
Exam 8: Roots, Radicals, and Root Functions358 Questions
Exam 9: Quadratic Equations, Inequalities, and Functions339 Questions
Exam 10: Inverse, Exponential, and Logarithmic Functions292 Questions
Exam 11: Nonlinear Functions, Conic Sections, and Nonlinear Systems233 Questions
Exam 12: Further Topics in Algebra190 Questions
Exam 13: Appendices29 Questions
Select questions type
Solve the equation. Use natural logarithms. When appropriate, give solutions to three decimal places unless otherwise indicated.
-
(Multiple Choice)
4.7/5  (32)
(32)
A city is growing at the rate of annually. If there were residents in the city in 1994 , find how many (to the nearest ten-thousand) were living in that city in 2000. Use
(Multiple Choice)
4.7/5  (28)
(28)
Use the horizontal line test to determine if the function is one-to-one.
-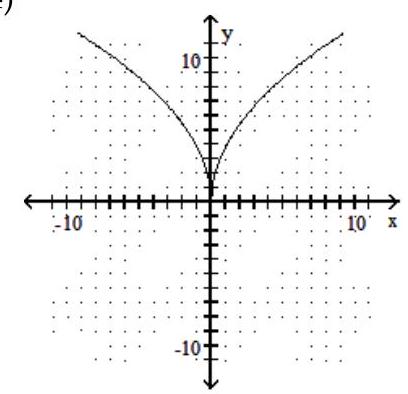
(True/False)
4.9/5  (31)
(31)
A classmate missed the lecture concerning the power rule of logarithms. When your classmate calls you on the phone for an explanation of why it works, what should you say to explain it?
(Essay)
4.8/5  (29)
(29)
Find the amount of money in an account after 11 years if is deposited at annual interest compounded quarterly. Assume no money is withdrawn.
(Multiple Choice)
4.9/5  (27)
(27)
Rewrite the given expression as a single logarithm. Assume that all variables are defined in such a way that variable expressions are positive and bases are positive numbers not equal to 1 .
-
(Multiple Choice)
4.8/5  (37)
(37)
Explain how the graph of the function can be obtained from the graph of the functionf .
(Essay)
4.9/5  (31)
(31)
Rewrite the given expression as a single logarithm. Assume that all variables are defined in such a way that variable expressions are positive and bases are positive numbers not equal to 1 .
-
(Multiple Choice)
5.0/5  (32)
(32)
The total number of rabbits on a farmer's property, assuming unlimited resources and space, can be approximated by the function , where corresponds to the initial number of rabbits, and corresponds to the number of rabbits after one year, and so on. The function is graphed on a graphing calculator-generated screen. Interpret the meanings of and in the display at the bottom of the screen.
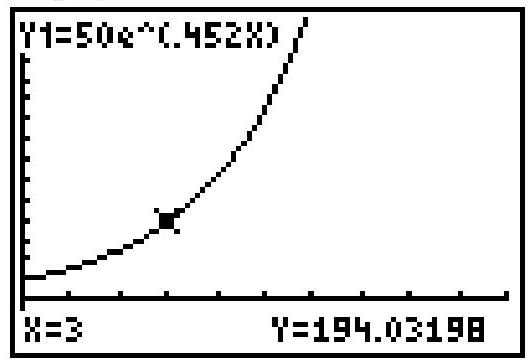
(Multiple Choice)
4.8/5  (32)
(32)
Express the given logarithm as a sum and/or difference of logarithms. Simplify, if possible. Assume that all variables represent positive real numbers.
-
(Multiple Choice)
4.8/5  (30)
(30)
Express the given logarithm as a sum and/or difference of logarithms. Simplify, if possible. Assume that all variables represent positive real numbers.
-
(Multiple Choice)
4.9/5  (34)
(34)
Use properties of logarithms to write each expression as a single logarithm. Assume that variables represent positive real numbers, with base .
-
(Multiple Choice)
4.8/5  (33)
(33)
Use the horizontal line test to determine if the function is one-to-one.
-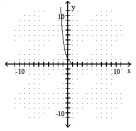
(True/False)
4.8/5  (40)
(40)
The number of bacteria growing in an incubation culture increases with time according to , where is time in days. After how many days will the number of bacteria in the culture be 563,200 ?(Hint: Let .)
(Multiple Choice)
4.8/5  (32)
(32)
Use properties of logarithms to write each expression as a single logarithm. Assume that variables represent positive real numbers, with base .
-
(Multiple Choice)
4.8/5  (33)
(33)
Showing 101 - 120 of 292
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)