Exam 6: Some Rules of Probability

Given mutually exclusive events $C$ and $D$ for which $P(C)=0.61$ and $P(D)=0.34$ , find - $P(C \cap D)$ .

A company has discovered a way of evaluating the success of both their radio and television advertising. If $R$ and $T$ are, respectively, the events that the radio advertising and television advertising are successful, $P(R)=0.62, P(T)=0.75$ , and $P(R \cap T)=\mathbf{0 . 4 3}$ . -Using the situation above, solve the following: $P\left(R^{\prime}\right)$ .

Two probabilities may be multiplied when we are asked

If $A$ and $B$ are two events, the probability that at least one of the two events occurs can be represented by $P(A \cup B)$ .

A company estimates that the probability of a recession occurring in the next year is 0.4 . The company also estimates the probability that another company distributes a competing product in the next year is 0.5 . Finally, the company feels that the probability of both a recession occurring and a competing product being produced in the next year is $\mathbf{0 . 2 5}$ . -In the situation above, if a company produces a competing product, find the probability that there will be a recession in the next year.

If the odds in favor of an event occurring is 9 to 2 , then the probability that the event will not occur is

A company estimates that the probability of a recession occurring in the next year is 0.4 . The company also estimates the probability that another company distributes a competing product in the next year is 0.5 . Finally, the company feels that the probability of both a recession occurring and a competing product being produced in the next year is $\mathbf{0 . 2 5}$ . -In the situation above, find the probability that there will be either a recession or a competing product or both in the next year.

In an experiment, persons are asked to pick a number from 10 to 18 , so that for each person the sample space is the set $S=\{10,11,12,13,14,15,16,17,18\}$ . If $A=\{10,11,15,16,17\}, B=\{10,12,14\}$ , and $C=\{14,16,18\}$ , list the elements of the sample space comprising each of the following events. - $A^{\prime}$

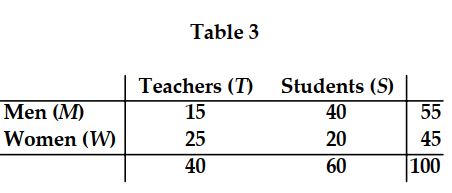-Using Table 3, the probability that a person is a male given that the person is a student is _______.

A school has tabulated the favorite snacks of 1000 of its students in the two categories, males and females. Here are the results: If one of the terms in the table above is selected at random, find each of the following probabilities. - $P(F \cup Z)=$ _______

A company has discovered a way of evaluating the success of both their radio and television advertising. If $R$ and $T$ are, respectively, the events that the radio advertising and television advertising are successful, $P(R)=0.62, P(T)=0.75$ , and $P(R \cap T)=\mathbf{0 . 4 3}$ . -Using the situation above, solve the following: $P(R \cup T)$ .

Two options an automobile buyer may purchase are air-conditioning $(C)$ and an automatic transmission $(T)$ . A dealer notes from his sales records that the probability of a buyer purchasing an automatic transmission is 0.60 and the probability that he purchased air-conditioning is 0.50 . The probability that the buyer bought air-conditioning if he bought an automatic transmission is 0.70 . -In the situation above, find the probability that a buyer purchased either air-conditioning or an automatic transmission.

If $A$ and $B$ are mutually exclusive events with $P(A)=\frac{1}{7}, P(B)=\frac{2}{7}$ , then $P(A \cup B)$ equals

A company has discovered a way of evaluating the success of both their radio and television advertising. If $R$ and $T$ are, respectively, the events that the radio advertising and television advertising are successful, $P(R)=0.62, P(T)=0.75$ , and $P(R \cap T)=\mathbf{0 . 4 3}$ . -Using the situation above, state in words what probability is expressed by the following: $P\left(R \cup T^{\prime}\right)$ .

Thirty percent of students attending a certain student mixer meet someone new to date. Forty percent of students attending the mixer dance at sometime during the mixer. Of those who dance, $60 \%$ meet someone new to date. A student who attends the mixer is randomly selected. -In the situation above, if $M$ is the event of meeting someone new and $D$ is the event of a student dancing, determine by calculation using a formula whether $M$ and $D$ are independent.

Given the sample space $S=\{1,2,3,4,5,6,7,8\}$ with $A=\{3,5,7\}, B=\{2,3,4,5,6\}$ , then $A^{\prime} \cap B=$ _______.

If the probability that a company will make a profit or break even is $\frac{2}{7}$ , then the odds in favor of the company losing money are _______.

A company has discovered a way of evaluating the success of both their radio and television advertising. If $R$ and $T$ are, respectively, the events that the radio advertising and television advertising are successful, $P(R)=0.62, P(T)=0.75$ , and $P(R \cap T)=\mathbf{0 . 4 3}$ . -Using the situation above, solve the following: $P\left(R \cap T^{\prime}\right)$ .

Thirty percent of students attending a certain student mixer meet someone new to date. Forty percent of students attending the mixer dance at sometime during the mixer. Of those who dance, $60 \%$ meet someone new to date. A student who attends the mixer is randomly selected. -In the situation above, find the probability that he/she has neither danced nor met someone new to date.

If the probability of an event $A$ is unaffected by the probability of an event $B$ , then the events $A$ and $B$ are mutually exclusive.