Exam 6: Some Rules of Probability

A company estimates that the probability of a recession occurring in the next year is 0.4 . The company also estimates the probability that another company distributes a competing product in the next year is 0.5 . Finally, the company feels that the probability of both a recession occurring and a competing product being produced in the next year is $\mathbf{0 . 2 5}$ . -In the situation above, let $R=$ recession occurs during the next year and $C=$ competing product is available in the next year. Using an appropriate formula, determine whether the events $R$ and $C$ are independent.

In an experiment, persons are asked to pick a number from 10 to 18 , so that for each person the sample space is the set $S=\{10,11,12,13,14,15,16,17,18\}$ . If $A=\{10,11,15,16,17\}, B=\{10,12,14\}$ , and $C=\{14,16,18\}$ , list the elements of the sample space comprising each of the following events. - $A^{\prime} \cap B$

A company has discovered a way of evaluating the success of both their radio and television advertising. If $R$ and $T$ are, respectively, the events that the radio advertising and television advertising are successful, $P(R)=0.62, P(T)=0.75$ , and $P(R \cap T)=\mathbf{0 . 4 3}$ . -Using the situation above, solve the following: $P\left(R \cup T^{\prime}\right)$ .

If $A$ and $B$ are independent events with $P(A)=0.25, P(B)=0.30$ , then $P\left\{(A \cup B)^{\prime}\right\}$ equals _______.

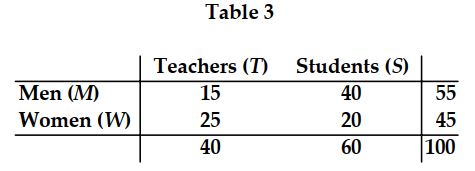-Using Table 3, the probability that a person is a woman, given that the person is not a teacher is

Three families A, B, and C, are bidding on the same one -family house. The probabilities are $0.20,0.25$ , and 0.28 , respectively, that a given family eventually moves into the house. -In the situation above, find the probability that none of the three families eventually moves into the house.

A basketball coach plans to add two players from among five juniors and eight seniors. What is the probability that -both people will be seniors?

Which of the following may be true if $A$ and $B$ are dependent events?

Two events are independent if they cannot both occur at the same time.

A vocational counselor believes that the probability that interest rates will go up is 0.40 . He further believes that the probability that a particular student will get a job at the end of the year if interest rates go up is 0.30 . Based on these estimates, the probability that both interest rates will go up and that the student will get the job is _______.

Given mutually exclusive events $C$ and $D$ for which $P(C)=0.61$ and $P(D)=0.34$ , find - $P(C \cup D)$ .

Two options an automobile buyer may purchase are air-conditioning $(C)$ and an automatic transmission $(T)$ . A dealer notes from his sales records that the probability of a buyer purchasing an automatic transmission is 0.60 and the probability that he purchased air-conditioning is 0.50 . The probability that the buyer bought air-conditioning if he bought an automatic transmission is 0.70 . -In the situation above, determine, using an appropriate formula, whether the events $C$ and $T$ are independent.

The expression $P(A \cup B)=P(A)+P(B)$ is valid if

If $A$ and $B$ are independent events, with $P(A)=\frac{1}{5}, P(B)=\frac{2}{5}$ , then $P(A \cup B)$

A school has tabulated the favorite snacks of 1000 of its students in the two categories, males and females. Here are the results: If one of the terms in the table above is selected at random, find each of the following probabilities. - $P\left(M^{\prime} \mid Z\right)=$ _______