Exam 15: Analysis of Variance
Exam 1: Introduction37 Questions
Exam 2: Summarizing Data: Listing and Grouping63 Questions
Exam 3: Summarizing Data: Measures of Location57 Questions
Exam 4: Summarizing Data: Measures of Variation56 Questions
Exam 5: Possibilities and Probabilities63 Questions
Exam 6: Some Rules of Probability75 Questions
Exam 7: Expectations and Decisions49 Questions
Exam 8: Probability Distributions78 Questions
Exam 9: The Normal Distribution89 Questions
Exam 10: Sampling and Sampling Distributions61 Questions
Exam 11: Problems of Estimation13 Questions
Exam 12: Tests of Hypotheses: Means55 Questions
Exam 13: Tests of Hypotheses: Standard Deviations39 Questions
Exam 14: Tests of Hypotheses Based on Count Data43 Questions
Exam 15: Analysis of Variance49 Questions
Exam 16: Regression39 Questions
Exam 17: Correlation28 Questions
Exam 18: Nonparametric Tests41 Questions
Select questions type
In testing the null hypotheses , the computed value is found by calculating
(Multiple Choice)
4.9/5  (39)
(39)
A new all-purpose cleaner is placed in four different locations in a supermarket. We would like to evaluate whether there is a significant difference in the number of cans sold with regard to location. The sample data below gives the number of cans sold in randomly selected supermarkets during a one-week period.
 a. Complete the one-way ANOVA table.
b. Test whether there is a significant difference in sales of the all-purpose cleaner with regard to location. Use .
a. Complete the one-way ANOVA table.
b. Test whether there is a significant difference in sales of the all-purpose cleaner with regard to location. Use .
(Essay)
4.8/5  (36)
(36)
A marketing researcher wants to evaluate the success (based on resulting sales) of three different marketing strategies (I, II, III) employing three different media (radio, television, and newspapers) in three different cities: Chicago, New York, and Los Angeles.
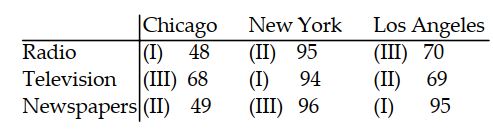 Analyze this Latin Square using the 0.05 level of significance for each test.
Analyze this Latin Square using the 0.05 level of significance for each test.
(Essay)
4.8/5  (36)
(36)
The __________ sum of squares measures the variation between samples.
(Short Answer)
4.8/5  (35)
(35)
In a one-factor ANOVA having three treatment levels with five observations in each sample, the within-samples degrees of freedom equals
(Multiple Choice)
4.9/5  (31)
(31)
In a one-way analysis of variance, the null hypothesis is rejected if the obtained value is greater than the tabled value.
(True/False)
4.9/5  (37)
(37)
In a one-way ANOVA, in terms of other sums of squares, __________.
(Short Answer)
4.9/5  (41)
(41)
The ratio which evaluates the significance of an extraneous variable in an analysis of variance is
(Multiple Choice)
4.8/5  (35)
(35)
If each kind of treatment appears with each kind of treatment once within the same block, the design is referred to as the __________ design.
(Multiple Choice)
4.8/5  (29)
(29)
If the null hypothesis in a one-way ANOVA is true, the between-samples variation is probably __________ the within-samples variation.
(Multiple Choice)
4.9/5  (38)
(38)
Find if the degrees of freedom for treatments is 4 and the degrees of freedom for error is 12.
(Short Answer)
4.9/5  (39)
(39)
In a Latin Square experiment, there are always __________ factors.
(Short Answer)
4.8/5  (39)
(39)
A two-factor ANOVA is being used to evaluate two null hypotheses. The first factor has 5 levels and the second has 4 levels.
The following data are obtained: .
a. Construct the ANOVA table
b. The two null hypotheses of equal means are tested at . What are the conclusions?
(Essay)
4.8/5  (37)
(37)
The formula for SST in a two-factor experiment is the same as for a complete-block experiment.
(True/False)
4.7/5  (36)
(36)
A Latin Square experiment is an example of a complete factorial experiment.
(True/False)
4.9/5  (38)
(38)
Showing 21 - 40 of 49
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)