Exam 9: Small Sample Inferences for Normal Populations

Find the probability of when d.f. = 21.

Consider the total number of points scored in a football game. The sum of both teams scores from 20 football games randomly selected from one National Football League season are: 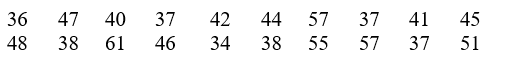Do these data substantiate a claim that the mean sum of points is greater than 40 points? Test with $\alpha$ =0.05.

The weights from a random sample of 16 adult golden doodle dogs have mean 66.4 pounds and standard deviation 4.8 pounds. As- sume that the weights of the dogs have a normal distribution. Ob- tain a 95 % confidence interval for the population standard devia- tion ?

Find the number b so that P[T < b] = .975 when d.f. = 6.

To check on the five second rule, a student drops a slice of ripe wa- termelon on an inoculated piece of wood flooring. After 5 seconds, the amount of bacteria transferred is measured in percent transfer. This experiment is repeated nine more times. According to one formula for the percent transfer X, the summary statistics are n = 10 $\bar{x}$ = 1.56 s = .08 Let µ =population mean transfer. (a) Conduct a test of hypotheses with the intent of showing that µ /= 1.5. Take $\alpha$ = .05. (b) Explain your choice of sampling distribution and any assump- tion you made concerning the population distribution. (c) Sketch the null distribution of your statistic and the rejection region. (d) Based on the conclusion to your test in Part a, what error could you have made?

A student documents a slow internet by observing the time , in minutes, that it takes to download five different web pages. 1 5 3 1 5 Let µ =population mean time in minutes. (a) Formulate the hypotheses when the intent of the test is to show that µ /= 2. (b) Assuming that the download time has a normal distribution, conduct a test of hypotheses. Take α = .10 (c) Based on the conclusion to your test in Part a, what error could you have made.

A naturalist measures the wing span of four butterflies. The data are 5 9 5 5 Let µ =population mean wingspan in centimeters. (a) Formulate the hypotheses when the intent of the test is to show that µ > 4.2. (b) Assuming that wing span has a normal distribution, conduct a test of hypotheses. Take α = .10 (c) Based on the conclusion to your test in Part a, what error could you have made. (d) Explain why this possible error will seldom occur.

According to health professionals, the incubation period for swine flu (the time between infection and appearance of symptoms) can be up to seven days, but it is most likely to be between two and five days. Recorded here are the incubation periods for seven infected persons. 5 4 2 4 5 6 5 Stating any assumption that you make, determine a 98% confidence interval for the true mean incubation period of this flu. Round your answer to two decimal places.

The following data shows the duration (in days) of eight randomly selected space shuttle missions. Test the null hypothesis that the mean duration of a space shuttle mission is 13 days versus a two-sided alternative. Take $\alpha$ =0.05

For one country, the mean emissions of sulphur dioxide SO₂ (thousands of tons) was measured for 17 years. The yearly average was 7706 thousands of tons, with standard deviation 1582 thousands of tons. Compute a 95% confidence interval for the mean number of emissions of SO₂ .

From a random sample of size 14, one has calculated the 98% confidence interval for $\mu$ and obtained the result (18.0, 24.2). What was the $\bar{x}$ for the sample?

Find the probability of T < -1.321 when d.f. = 22.

Using the table for the t distributions, find the upper 0.005 point when d.f. = 1.

The weights from a random sample of 21 Irish setter dogs have mean 61.7 pounds and standard deviation 5.8 pounds. Assume that the weights of the dogs have a normal distribution. A) Construct a 95% confidence interval for the population. B) What is the center of this confidence interval?

Find the probability of | T | > 1.812 when d.f. = 10.

Using the table for the t distributions, find the 99th percentile of the t distribution when d.f. = 2.

A random sample of size 12 from a normal population produced a 95% confidence interval (182.4, 191.2) based on the t distribution. What is the conclusion of the t test for H₀: $\mu$ =179.1 versus H₁: $\mu$$\neq$ 179.1?

The weights from a random sample of 16 adult golden doodle dogs have mean 66.4 pounds and standard deviation 4.8 pounds. As- sume that the weights of the dogs have a normal distribution. Let µ =population mean number of times. (a) Conduct a test of hypotheses with the intent of showing that µ > 63 pounds. Take $\alpha$ = .05. (b) Explain your choice of sampling distribution and any assump- tion you made concerning the population distribution. (c) Sketch the null distribution of your statistic and the rejection region. (d) Based on the conclusion to your test in Part a, what error could you have made?

The length (in seconds) of cellular phone calls in an industrial zone has a normal distribution. Suppose that, from a random sample of lengths, the t based 90% confidence interval for the population mean length is (83.4, 109.7) seconds. On the basis of the same sample, would H₀: $\mu$ =83.8 be rejected in favor of H₁: $\mu$$\neq$ 179.1 at $\alpha$ =0.01? Answer the question "Yes", "No", or Cannot tell".

From a random sample of size 18, one has calculated the 95% confidence interval for $\mu$ and obtained the result (18.6, 24.0). What was the s for the sample?